| The
graph of a function |
| The
graph of a function f
is drawing on the Cartesian plane, plotted with respect to
coordinate axes, showing functional relationship between given
variables containing all those points (x,
f (x))
which satisfy the given relation. |
| The points lying on the curve
satisfy this relation that determines the shape of the graph. |
| The
graphic representation of a function provides insight into the behavior of the
function. |
|
| Functions
behavior, properties
and characteristic points of the graph |
| To
sketch the graph of a function we should know
its properties and determine its characteristic points, as |
|
- domain and range |
|
- x-intercepts or zeros (roots) and
the y-intercept |
|
- intervals of
increasing and decreasing |
|
- continuity and discontinuity |
|
- vertical, horizontal and oblique or slant asymptotes |
|
- turning points (extremes, local or relative maximums
or minimums)
|
|
-
inflection points and intervals of concavity |
|
- symmetry (odd and even
functions) with respect to the x-axis,
y-axis, and the origin |
|
|
Domain and range |
|
The domain is
the set of values of the independent variable of a given function,
i.e., the set of all first members of the ordered pairs (x,
f (x))
that
constitute the function. |
|
The range is
the set of values that given function takes as its argument varies
through its domain. It is the image of the domain. |
|
The codomain
is the set within which the values of a function lie, as opposed to
the range, which is the set of values that the function actually
takes. |
|
Therefore, the range must be a subset of,
but may or may not be identical with the codomain. |
|
We will only consider real-valued
functions of a real variable. |
|
|
Roots or zero function
values, x-intercepts, y-intercepts |
| A
zero of a function is a value of the argument of a function at
which the value of the function is zero. |
| An
intercept
is the point at which a given function intersects with specified
coordinate axis, or the value of that coordinate at that point. |
| An
x-intercept
is the point (x,
0)
where the graph of the function touches or crosses the x-axis. |
| That
is, at the x-intercept,
the coordinate y
= 0. |
| A
zero of a function is the x
value of the x-intercept.
The
zeros (roots) of a function correspond to the x-intercepts
of the graph. |
| The
y-intercept
is the value of y
where the graph crosses the y-axis. |
| The
y-intercept
correspond to the point (0,
y) on
the y-axis
therefore,
at the
y-intercept
the coordinate x
= 0. |
|
|
Increasing/decreasing
intervals |
| A
function ƒ
is increasing on an interval if |
| f
(x1)
< f (x2)
for each x1
< x2
in
the interval. |
| A
function ƒ
is decreasing on an interval if |
| f
(x1)
> f (x2)
for each x1
< x2
in
the interval. |
| By looking at the graph of a function being traced out as the value of the input
variable x
increases from left to right then, if at the same time the output value
y
=
f (x) also increases, we say the function is increasing. |
| If the output value decreases as
x
increases, then we say the function f
is
decreasing. |
|
| Thus,
if the slope or gradient m
of the secant line passing through the points (x1,
f (x1))
and (x2,
f (x2))
of the graph of a function |
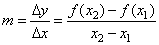 |
| where,
x2
-
x1>
0 |
| |
|
|
 |
|
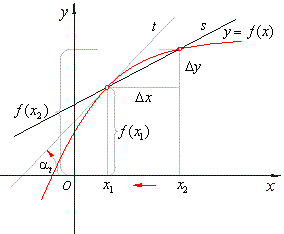
| is
positive, the function is increasing (going up), as shows the
figure above. |
| Since
the difference x2
-
x1 is
always positive, when the function is decreasing (going down), the slope will be negative. |
| The
ratio of the rise and the run, called the difference quotient,
that equals the value of the tangent of the angle between the
direction of the secant line and x-axis,
becomes the slope (gradient) of the tangent line as the difference Dx
tends to zero, and is called the instantaneous
rate of change or the derivative
at the point of the function. |
|
For
a given function f
and point
(x1,
f (x1)), the
derivative of f
at
x
= x1
is the slope of the tangent line through the point (x1,
f (x1)),
i.e., f
'(x1)
= tan
at
. |
|
| Continuity and discontinuity |
| A
function that has no sudden changes in value as the variable
increases or decreases smoothly is called continuous function. |
| Or
more formally, a real function y
=
f (x)
is continuous at a point a
if the limit of f
(x)
as x
approaches a
is f (a). |
| If
a function does not satisfy this condition at a point it is said
to be discontinuous, or to have a discontinuity
at that point. |