|
| Conic
Sections |
|
|
|
|
Hyperbola
|
|
Examples of hyperbola |
 Equilateral or rectangular hyperbola with the coordinate axes as its
asymptote
Equilateral or rectangular hyperbola with the coordinate axes as its
asymptote
|
|
Translation
of equilateral or rectangular hyperbola with the coordinate axes as its
asymptote |
|
|
|
|
|
|
| Examples
of hyperbola |
Example:
Given is the hyperbola
4x2 -
9y2 = 36,
determine the semi-axes, equations of the asymptotes,
coordinates of foci, the eccentricity and the semi-latus rectum.
|
Solution:
Put the equation in the standard form to
determine the semi-axes, thus
|
|
4x2
-
9y2 = 36 | ¸
36
|
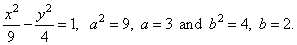
|
| Asymptotes, |
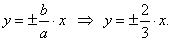 |
|
| Applying, |
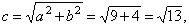 |
|
|
coordinates of foci, F1(-Ö13,
0) and
F2(Ö13,
0).
|
|
 |
|
| The eccentricity, |
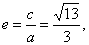 |
and the
semi-latus rectum,
|
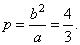 |
|
|
| Example:
Write equation of a hyperbola with the focus at
F2(5,
0) and whose asymptotes are, |
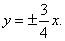 |
|
|
|
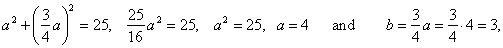 |
| Therefore,
the equation of the hyperbola,
|
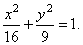 |
|
|
|
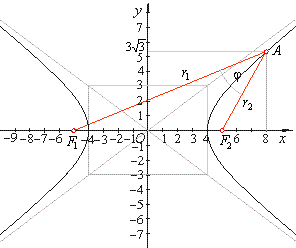
| Example:
Find the angle subtended by the focal radii
r1
and
r2
at a point A(8, y
> 0) of the hyperbola
|
| 9x2
-
16y2 = 144. |
|
Solution:
We determine the ordinate of the point
A
by plugging its abscissa into equation of the hyperbola,
|
|
x
= 8 =>
9x2
-
16y2 = 144
|
|
9 · 82
-
16y2 = 144,
|
|
16y2 = 432 =>
y2 =
27,
|
|
y1,2 = ±3Ö3
so that A(8,
3Ö3).
|
|
The equations of the lines of the radii r1
and
r2, we
write
using the formula of a line through two
points. Since,
|
| r1::
AF1 and
F1(-c,
0) ,
and |
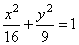 |
|
| then |
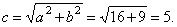 |
|
|
 |
|
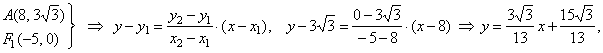 |
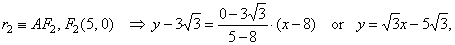 |
|
Therefore, the angle between the focal radii r1
and
r2
at the point A
of the hyperbola, as
|
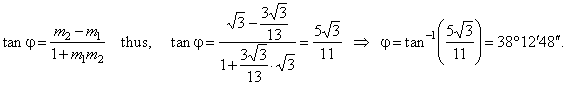 |
|
| Equilateral or rectangular hyperbola with the coordinate axes as its
asymptote
|
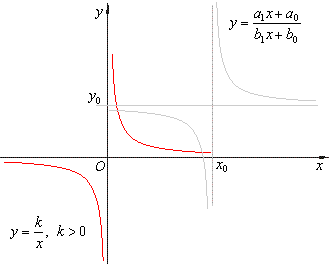
| The
graph of the reciprocal function y
= 1/x or y
= k/x is a rectangular
(or right) hyperbola of which asymptotes are the coordinate axes. |
| If k
> 0 then, the
function is decreasing from zero to negative infinity
and from positive infinity to zero, i.e., the graph of
the rectangular hyperbola opening in the first and third
quadrants as is shown in the right figure. |
| The vertices, |
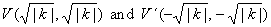 |
|
|
|
 |
|
|
| Translation
of equilateral or rectangular hyperbola with the coordinate axes as its
asymptote |
| The rational function |
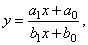 |
by dividing the
numerator by denominator, |
|
| can be
rewritten into |
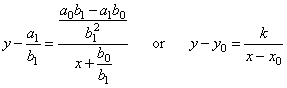 |
where, |
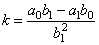 |
|
| is the constant, |
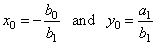 |
are the vertical and
the horizontal asymptote respectively. |
|
| Therefore,
the values of the vertical and the horizontal asymptotes correspond to
the coordinates of the horizontal and the vertical translation of the
reciprocal function y
= k/x as is shown in
the figure below. |
 |
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |