|
| Conic
Sections |
|
|
|
|
|
Ellipse
|
 Definition and construction
Definition and construction |
|
Eccentricity and linear
eccentricity
|
|
Constructions of an ellipse |
 Equation of the ellipse, standard
equation of the ellipse
Equation of the ellipse, standard
equation of the ellipse
|
|
The equation of the ellipse examples |
|
|
|
|
|
|
| Definition and construction, eccentricity and linear
eccentricity
|
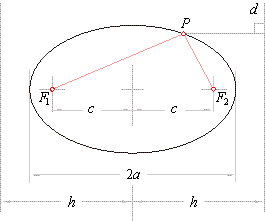
| An ellipse is the set of points (locus) in a plane whose distances from two fixed points have a constant sum. |
|
The fixed points F1
and F2 are called foci. Thus, the sum of distances
of any point P, of the ellipse, from the
|
| foci is
|
F1P |
+
|
F2P | =
2a, and the
distance between foci |
F1F2 | =
2c, |
| where 2a is the
major
axis,
2c is called
focal distance and
c
is also called linear
eccentricity. |
| Quantities
a
and c,
a
> c,
uniquely determine an ellipse. The ratio e = c/a,
e < 1
is called eccentricity
of the ellipse. |
| The ellipse can also be defined as the locus of points the ratio of whose distances from the
focus to a vertical line, known as the
directrix ( d
), is a constant
e,
where |
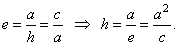 |
|
 |
|
|
| Constructions of an ellipse |
| According to
definition we
will explain two constructions of the ellipse: |
|
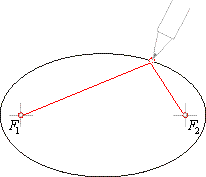
| -
Fasten the ends of a string of length
2a
> 2c
at two distinct points F1 and
F2. |
|
Pull the loop of string tight using the pencil until a triangle is formed with the pencil and the two foci as vertices. |
|
Keeping the string pulled tight, move the pencil around until the ellipse is traced out. |
|
 |
|
|
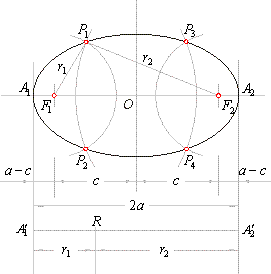
| - On a given line segment
A1'
A2'
= 2a, of the major
axis, choose an arbitrary point R.
|
|
Draw an arc of the radius A1'R
= r1
with center F1
and then draw an arc with center F2
and radius A2'R
= r2, intersecting the arc at points P1 and
P2. |
Repeat the same procedure by drawing the arc of the radius
r1
centered at F2
and the arc of the radius
r2
with
the center F1 to obtain intersections
P3 and
P4.
|
|
Using this method we can draw as many points of the ellipse as needed, noticing that while choosing point R, always must be
r1
> a -
c and r2
>
a -
c. |
|
This construction shows that the ellipse has two axes of symmetry of different length, the
major and
minor axes. Their intersection is the center of the ellipse. |
|
 |
|
|
| Equation of the ellipse, standard
equation of the ellipse
|
| If in the direction of axes we introduce a coordinate system so that the center of the ellipse coincides with the |
|
origin, then coordinates of foci are |
| F1(-c, 0) and
F2(
c, 0). |
| For every
point P(x,
y) of the ellipse, according to |
| definition
r1 + r2 =
2a, it follows
that |
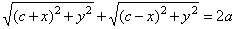 |
| after
squaring |
|
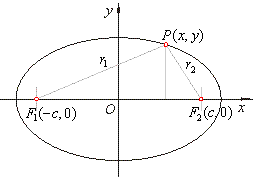 |
|
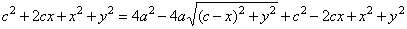 |
| and
reducing |
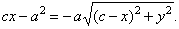 |
|
| Repeated squaring and grouping gives |
| (a2
-
c2) · x2
+ a2y2 = a2
· (a2 -
c2), |
|
|
| follows |
b2x2
+ a2y2 = a2b2 |
equation
of the ellipse, |
|
|
 |
|
| and after division by
a2b2, |
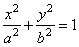 |
standard equation of the ellipse. |
|
|
It follows from the equation that an ellipse is defined by values of
a
and b, or as they are associated through
the relation a2
-
c2 = b2,
we can say that it is defined by any pair of these three quantities. |
| Intersections of an ellipse and the coordinate axes we determine from equation |
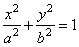 |
by
putting, |
|
| y
= 0 =>
x
= + a,
so obtained are vertices at the ends of the major axis A1(-a,
0) and
A2(a,
0), and |
| x
= 0 =>
y = + b,
obtained are co-vertices, the endpoints of the minor axis B1(0,
b) and
B2(0,
-b). |
The line segments
A1A2
= 2a and
B1B2
= 2b are the
major and
minor axes while
a and b
are the
semi-major and
semi-minor axes respectively. So the arc of the radius
a
centered at B1and
B2 intersects the major axis at
the foci F1and
F2. |
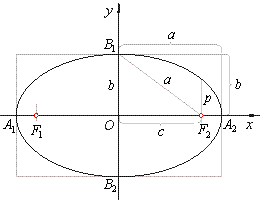
The focal parameter, called latus rectum and denoted
2p, is the chord perpendicular to the major axis
passing through any of the foci, as shows the above figure. The length of which equals the absolute value of ordinates of the points of the ellipse whose abscissas x
= c
or x
= -c
that is |
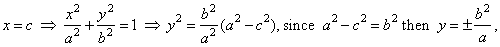 |
| so
the length of the latus rectum |
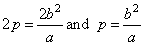 |
the
length of the semi-latus rectum of the ellipse. |
|
|
| The
equation of the ellipse examples |
| Example:
Given is equation of the ellipse
9x2
+ 25y2 = 225, find the lengths of semi-major and
semi-minor axes, coordinates of the foci, the eccentricity and the length of the
semi-latus rectum. |
| Solution: From the standard equation |
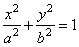 |
we can find the semi-axes
lengths dividing the given |
|
| equation by
225, |
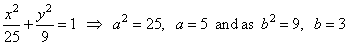 |
|
|
coordinates of the
foci F1(-c, 0) and
F2(
c, 0),
since
|
 |
 |
|
| Example:
From given quantities of an ellipse determine remaining unknown quantities and write equation
of the ellipse, |
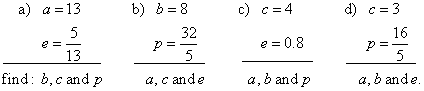 |
| Solution:
a) Using |
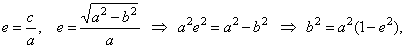 |
|
| therefore,
the semi-minor axis |
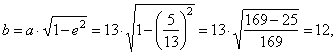 |
|
| the
linear eccentricity |
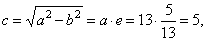 |
|
| the
semi latus rectum |
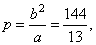 |
and
the equation of the ellipse |
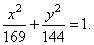 |
|
|
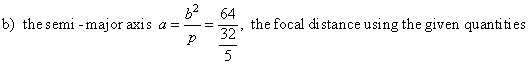 |
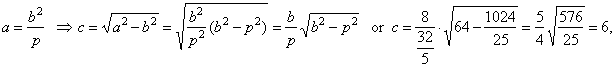 |
| the eccentricity |
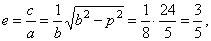 |
and
the equation of the ellipse |
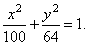 |
|
|
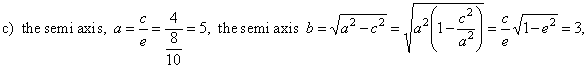 |
| the
semi latus rectum |
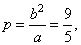 |
and
the equation of the ellipse |
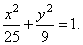 |
|
|
|
d) unknown quantities expressed through given values, |
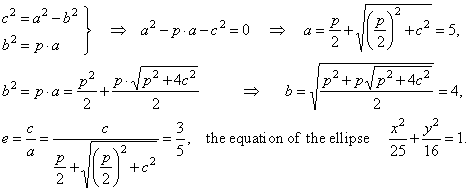 |
|
| Example:
Find the equation of
the ellipse whose focus is F2(6,
0) and which passes through the point
A(5Ö3,
4). |
| Solution:
Coordinates of the point
A(5Ö3,
4) must satisfy equation of the ellipse, therefore |
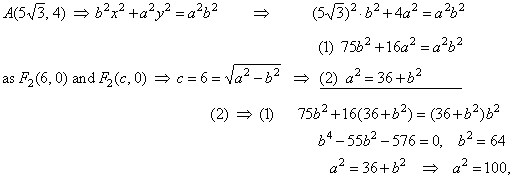 |
|
thus,
the equation of the ellipse |
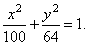 |
|
|
|
| Example:
Write equation of the ellipse passing through points
A(-4,
2) and B(8,
1). |
| Solution:
Given points must satisfy equation of the ellipse, so |
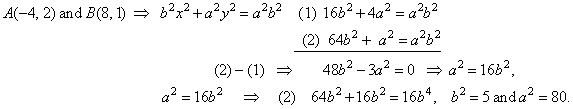 |
| Therefore,
the equation of the ellipse |
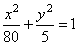 |
or
x2
+ 16y2 = 80. |
|
|
|
|
|
|
|