|
| Conic
Sections |
|
|
|
 Conics,
a Family of Similarly Shaped Curves - Properties of Conics
Conics,
a Family of Similarly Shaped Curves - Properties of Conics |
 Conics - a family of similarly shaped curves
Conics - a family of similarly shaped curves |
|
|
|
|
|
|
| Conics, a
family of similarly shaped curves
- properties of conics |
|
By intersecting
either of the two right circular conical surfaces (nappes) with the plane perpendicular to the
axis of
the cone the resulting intersection is a circle
c, as
is shown in the figure. |
|
|
When the cutting plane is inclined to the axis of the cone at a greater angle than that made by
the generating segment or generator (the slanting edge of the cone), i.e., when the plane cuts all
generators of a single cone, the resulting curve is the
ellipse
e.
|
| Thus, the circle is a special case
of the ellipse in which the plane is perpendicular to the axis of the cone.
|
|
|
If the cutting plane is parallel to any generator of one of the cones, then the intersection curve is
the
parabola
p.
|
|
|
When the cutting plane is inclined to the axis at a smaller angle than the generator of the cone,
i.e., if the intersecting plane cuts both cones the
hyperbola
h
is generated.
|
|
 |
|
|
|
| Conics - a family of similarly shaped curves |
| A conic is the set of points
P
in a plane whose distances from a fixed point F
(the focus) and a fixed line d
(the directrix), are in a constant ratio. This ratio named the
eccentricity e
determines the shape of the curve.
|
| We can see that conics represent a family of similarly shaped curves if we write their equations in vertex
form.
|
Recall the method we used to transform equations of the ellipse and the hyperbola from standard to
vertex form. We placed the vertex of the curve at the origin translating its graph.
|
|
Thus, obtained are their vertex
equations;
|
| y2 =
2px -
(p/a)x2 |
| -
the
ellipse
and the
circle |
| (for
the circle p =
a = r) |
|
|
|
|
| y2 =
2px + (p/a)x2 |
| -
the
hyperbola |
|
|
|
Using geometric interpretation of
these
equations we compare the area of the square
y2, formed by the ordinate of a
point
P(x,
y), with the
area of the rectangle
2p · x, whose
one side is the abscissa
x
of the point P
and the parameter 2p
other side, it follows that
|
|
 |
|
|
- for the ellipse the area of the square is smaller, than the area of the rectangle,
|
|
- for the parabola is equal,
|
|
- for the hyperbola the area of the square is greater than the area of the rectangle.
|
| The names of curves were given as a result of the above relations,
so; |
|
- the word “ellipse” (elleipyis)
in Greek means “deficiency," |
|
- the word “parabola” (parabolh)
means “equality” and |
|
- the word “hyperbola” (uperbolh)
means “excess.” |
|
| In
the given vertex equations we can make following substitutions for; |
|
- the ellipse |
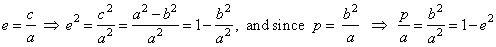 |
|
|
- the
circle |
p =
a = b = r
=> e
= 0 |
|
|
|
|
- the
hyperbola |
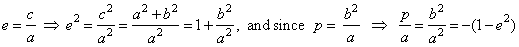 |
|
| Thus, the
equation of conics in vertex form is |
y2 =
2px -
(1 -
e2)x2.
|
|
|
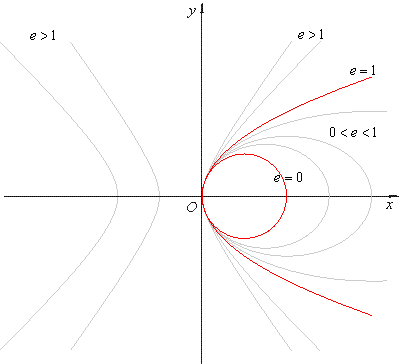
| The values of
e
define the curve the conic section makes, such that for |
|
e = 0
- a circle, |
|
0 < e < 1
- an ellipse, |
|
e = 1
- a parabola, |
|
e > 1
- a hyperbola, |
| as shows
the above figure. |