|
| Conic
Sections |
|
|
|
|
|
Circle
and Line
|
 Tangents to a circle from a point outside the circle - use of the
tangency condition
Tangents to a circle from a point outside the circle - use of the
tangency condition
|
 Angle between a line and a circle
Angle between a line and a circle
|
|
|
|
|
|
|
| Tangents to a circle from a point outside the circle - use of the
tangency condition
|
| Example:
Find the angle between tangents drawn from the point
A(-1,
7) to the circle
x2
+ y2 = 25 . |
| Solution:
Equations of tangents we
find from the system formed by equation of the line and the
tangency condition, |
|
A(-1,
7) => (1)
y =
mx + c => c =
m + 7
=> (2) |
|
(2) r2·(m2
+ 1)
= c2 |
|
|
|
25(m2
+ 1)
= (m + 7)2 |
| 12m2
-
7m
-
12 = 0 => m1
= -
3/4
and
m2
= 4/3 |
| c1
= -
3/4 + 7 = 25/4 and
c2
= 4/3 + 7 = 25/3 |
| therefore,
the equations of tangents, |
| t1
::
y =
-
(3/4)x + 25/4 and
t2
::
y =
(4/3)x + 25/3. |
| Slopes of tangents satisfy perpendicularity condition, that is
|
| m1
= -
1/m2
=>
j =
90°. |
|
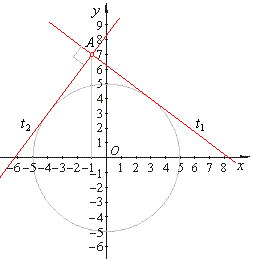 |
|
|
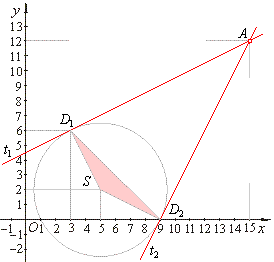
| Example:
Find the area of the triangle made by points of contact of tangents, drawn from the point |
| A(15,
12) to the circle
(x
-
5)2 + (y -
2)2 =
20 , and the center
S of the circle. |
Solution:
From the system of equations formed by equation of the line through point
A
and the condition of
tangency for the circle with the center at S(p,
q), we calculate slopes and intersections of tangents, thus |
| A(15,
12)
=> (1) y =
mx + c, c =
12 -
15m
=>
(2) |
|
(2) r2·(m2
+ 1) = (q -m
p -
c)2 |
|
|
|
S(5,
2)
and
r2
= 20
=>
(2) |
| 20·(m2
+ 1) = (2 -
5m
-
12 +
15m)2 |
| 2m2
-
5m
+ 2 = 0
=>
m1
= 1/2
and
m2
= 2, |
| as
c =
12 -
15m
then c1
= 9/2 and
c2
= -
18 |
| therefore,
the equations of tangents, |
| t1
::
y =
(1/2)x + 9/2
and
t2
::
y =
2x -
18. |
|
 |
|
| Coordinates of the tangency points we calculate
by solving system of equations formed by equations of tangents and equation of the
circle, thus |
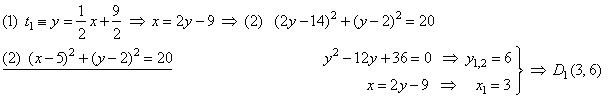 |
| and
the tangency point D2, |
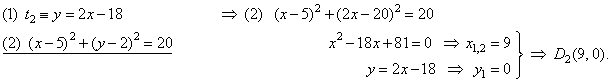 |
| The
area of the triangle SD1D2, |
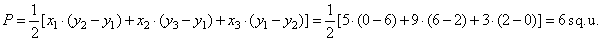 |
|
| Example:
Given is a line
-3x +
y + 1 = 0 and a circle
x2
+ y2 -
6x
- 4y
+ 3 = 0,
find equations of tangents to the circle which are perpendicular to the line. |
| Solution:
Slopes of tangents are determined by condition of
perpendicularity, therefore |
| y =
3x -
1,
m =
3
so that
mt =
-1/3 |
| x2
+ y2 -6x
-4 y
+ 3 = 0
=>
(x
-
3)2 + (y -
2)2 = 10 |
| thus,
S(3,
2)
and
r2
= 10. |
| To
find intersections c
we use the tangency condition, |
| r2·(m2
+ 1)
= (q -m
p -
c)2 |
| 10[(-1/3)2
+ 1]
= [2 -(-1/3)·3
-
c]2 or
(3
-
c)2
= 100/9 |
| (3
-
c)
= ± 10/3
so c1
= -1/3
and c2
= 19/3. |
| The equations of
tangents are, |
| t1
::
y =
-(1/3)x
-1/3 and t2
::
y =
-(1/3)x
+19/3. |
|
 |
|
|
| Example: Find equations of the common tangents to
circles x2
+ y2 =
13 and (x
+ 2)2 + (y +
10)2 =
117. |
| Solution:
Slopes and intersections of common tangents to the circles must satisfy tangency condition of both
circles. Therefore, values for slopes m
and intersections c
we calculate from the system of equations, |
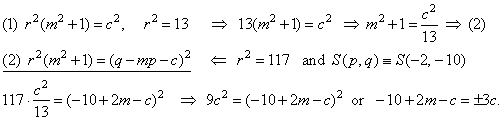 |
| The
equation -10
+ 2m -
c = +3c
does not satisfy given conditions. |
| The
equation -10
+ 2m -
c = -3c
or c = 5 -
m plugged into (1) |
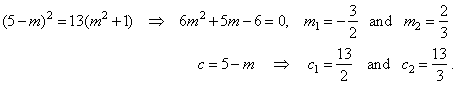 |
| Therefore,
the equations of the common tangents are, |
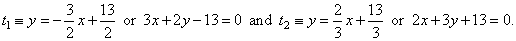 |
|
| Angle between a line and a circle
|
| The angle between a line and a circle is the angle formed by the line and the tangent to the circle at the
intersection point of the circle and the given line. |
|
| Example:
Find the angle between a line
2x +
3y -
1 = 0 and a circle
x2
+ y2 +
4x
+ 2y - 15
= 0. |
| Solution:
Coordinates of
intersections of the line and the circle calculate by solving the system, |
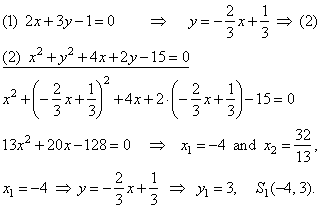 |
| Rewrite
the equation of the circle to standard form, |
| x2
+ y2 +
4x
+ 2y - 15
= 0
Þ
(x
-
p)2 + (y -
q)2 = r2 |
| thus,
(x +
2)2 + (y + 1)2 = 20,
S(-2,
-1) and
r2
= 20. |
|
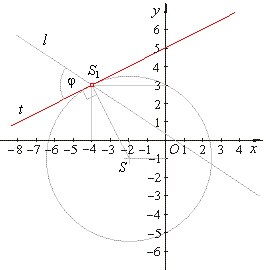 |
|
| Equation of the tangent at the intersection
S1, |
| S1(-4,
3)
=>
(x1 -
p) ·
(x -
p) + (y1 -
q) ·
(y -
q) = r2
|
| (-4
+
2)
· (x +
2)
+ (3 + 1)
·
(y
+
1)
= 20
=>
t
::
-
x
+ 2y
-
10
= 0
or y =
1/2x + 5 |
| The angle between the line and the circle is the angle formed by the line and the tangent to the circle at the
intersection point, therefore
|
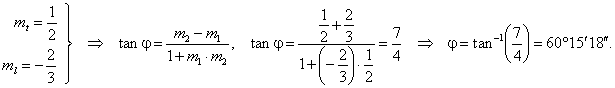 |
|
|
|
|
|
|