| |
| Algebraic
Expressions |
|
|
|
Factoring polynomials |
|
Using a variety of methods including combinations of the above to factorize
algebraic expressions |
|
|
|
|
|
|
|
|
|
| Factoring polynomials |
| A
polynomial and/or polynomial
function
f (x)
= anxn
+ an-1xn-1
+
. . . +
a1x
+ a0 |
| in
the variable x
with
real coefficients can be expressed as a product of its leading
coefficient an
and
n
linear |
|
factors of the form x
-
xi,
where xi
denotes its real roots and/or conjugate complex
roots, thus |
| f
(x)
= anxn
+ an-1xn-1
+
. . . +
a1x
+ a0
= an(x
- x1)(x
- x2)
. . . (x
- xn).
|
| By
multiplying the parentheses on the right side and collecting
like terms and then comparing the resulting coefficients with
the coefficients of the given polynomial obtained are Vieta's
formulas that show relations between coefficients and roots of a
polynomial. |
| Thus,
for a quadratic or a second
degree polynomial |
|
a2x2
+ a1x
+ a0 = a2(x
- x1)(x
- x2)
= a2[x2
-
(x1 +
x2)x
+
x1x2], |
|
|
|
| and
similarly, for a cubic or a third
degree polynomial |
|
a3x3
+ a2x2
+ a1x
+ a0 = a3(x
- x1)
(x
- x2)
(x
- x3)
= |
|
|
| |
=
a3[x3
-
(x1 +
x2
+
x3)x2
+
(x1x2 +
x1x3
+
x2x3)x
- x1x2x3]. |
|
|
|
Example:
|
Factorize
2/3x2
- 2/3x
- 4
using
the above theorem. |
| Solution: |
2/3x2
- 2/3x
- 4
=
2/3(x2
- x
- 6)
=
2/3[x2
- (3
+ (-
2))x
+ 3(-
2)] =
|
|
= 2/3(x2
- 3x
+ 2x
- 6)
=
2/3[x(x
- 3)
+ 2(x
- 3)]
=
2/3(x
- 3)(x
+ 2) |
|
|
|
Example:
|
Given
are leading
coefficient a2
=
-1and
the complex
roots,
x1 =
1 +
i
and
x2
=
1 -
i,
of
a |
|
second
degree polynomial, find
the polynomial using
the above theorem. |
| Solution: |
By
plugging the given values into a2x2
+ a1x
+ a0 = a2(x
- x1)
(x
- x2)
|
|
a2x2
+ a1x
+ a0 = -1[x
-
(1
+ i)]
· [x
-
(1 -
i)]
= -[(x
- 1)
-
i]
· [(x - 1)
+ i]
=
|
|
= -[(x - 1)2
-
i2]
=
-(x2
- 2x
+ 1 +
1)
=
- x2
+ 2x
- 2 |
|
|
|
Example:
|
The
real root of the polynomial -
x3
-
x2
+ 4x
- 6
is
x1 =
- 3,
factorize the polynomial. |
| Solution: |
We
divide given polynomial by one of its known
factors, |
|
a3x3
+ a2x2
+ a1x
+ a0 = a3(x
- x1)
(x
- x2)
(x
- x3) |
|
 |
|
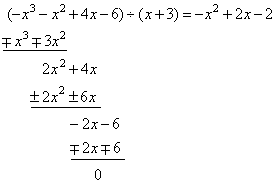then
we calculate another two roots of given cubic by solving
obtained quadratic trinomial, |
|
 |
|
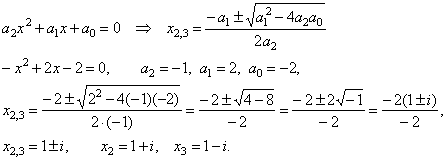Finally
we use the theorem to factorize given polynomial (see
the previous example), |
|
a3(x
- x1)(x
- x2)(x
- x3)
= -1(x
+ 3)[x
-
(1
+ i)][x
-
(1 - i)] |
|
= -
(x
+ 3)(x2
- 2x
+ 2). |
|
Notice that given cubic has one real root and the pair of the conjugate complex roots. |
|
Odd
degree polynomials must have at least one real root. |
|
|
| Using
a variety of methods including combinations of the above to
factorize algebraic expressions |
|
Examples:
|
|
a) x2
- 2xy
+ y2
+ 2y
- 2x
=
(x
- y)2
- 2(x
- y)
=
(x
- y)(x
- y
- 2), |
|
|
|
|
|
|
b) x2
- y2
+ xz
- yz
=
(x
- y)(x
+ y)
+ z(x
- y)
= (x
- y)(x
+ y
+ z), |
|
|
|
|
|
c) 4x2
- 4xy
+ y2
- z2
= (2x - y)2
- z2
=
(2x
- y
- z)(2x
- y
+ z), |
|
|
|
| d) a3
- 7a
+ 6
= a3 - a
- 6a
+ 6
= a(a2 -1)
- 6(a
-1)
= (a -1)·[a(a
+ 1)
- 6]
= (a -1)(a2
+ a
- 6)
= |
|
= (a -1)(a2
+ 3a
- 2a
- 6)
= (a -1)[a(a
+ 3)
- 2(a
+ 3)]
= (a -1)(a
+ 3)(a
- 2). |
|
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
