|
| Geometry
- Triangle Problems and Solutions |
|
|
 Triangle, solved problems, examples
Triangle, solved problems, examples |
|
|
|
|
|
|
| Example:
A circle with the center at the center of an equilateral triangle intersects all three sides of the triangle to three equal
parts each. Find the area of the parts of the triangle outside the circle if the side of the triangle
a =
Ö6. |
| Solution: Given,
a =
Ö6.
A
=
? |
|
|
| Example:
Lengths of sides of a right triangle are terms of an arithmetic
progression with the difference 2, find the radius of
incircle. |
| Solution: Given,
a = x,
b = x + 2
and c =
x + 4.
r = ? |
|
|
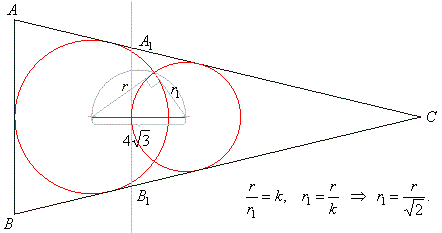
| Example:
A line parallel to the side AB, of a triangle
ABC, divides the triangle to two parts of the same
areas and intersects
the side AC at the point
A1 and the side
BC at the point
B1. If radii of incircles of triangles,
ABC and
A1B1C are at
the same time legs of a right triangle whose hypotenuse length is
4Ö3, find the radius of the incircle of the
triangle ABC. |
| Solution: |
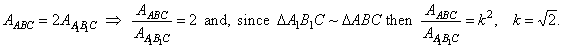 |
|
 |
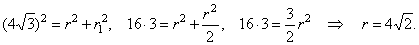 |
| Example:
In a right triangle ABC, with the angle
90°
at C, the altitude from vertex
C
to the hypotenuse AB
meets the
hypotenuse at the point D. If both radii of incircles of triangles
ACD and
BCD are equal and measure
2Ö2
cm, find the radius
(r)
of the incircle of the triangle
ABC. |
| Solution: Given,
r1 =
2Ö2
cm.
r = ? |
|
|
| Example:
In a right triangle ABC, with the angle
90°
at C, the altitude from vertex
C
to the hypotenuse AB
meets the
hypotenuse at the point D. If radii of incircles of triangles
ACD and
BCD are,
1
cm and 2Ö2
cm rspectively, find
the radius of the incircle of the triangle ABC. |
| Solution: Given,
r1 =
1 cm and
r2 =
2Ö2
cm.
r = ? |
| Since,
DABC
~ DACD
~ DBCD
then,
|
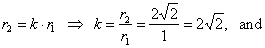 |
|
|
|
| Example:
Lengths of sides of a triangle are in the proportion 9
: 10 : 17, find the radius of the incircle if the
difference of the
longest and the shortest side is 16
cm. |
| Solution:
Given,
a
: b : c = 9 : 10 : 17 and
c
-
a = 16
cm.
r = ? |
|
|
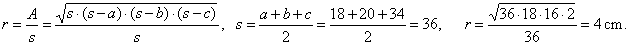 |
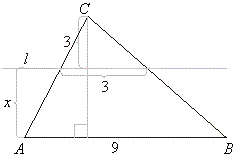
| Example:
The side AB
of a triangle ABC
is 9
cm long. Sides, AC
and BC, form on a line
l, which is
parallel to side AB, the
segment 3
cm long. If the distance of the vertex C from the line
l is
3
cm, find the distance of the line l from the
side AB. |
| Solution:
As shown triangles
are similar following proportion must hold, |
 |
|
9 : 3 = (3 + x) : 3 |
| 3
· (3 + x) = 3 · 9 |
|
3 + x = 9 |
|
x = 6 cm. |
|
|
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |