|
| Geometry
- Triangle Problems and Solutions |
|
|
 Triangle, solved problems, examples
Triangle, solved problems, examples |
|
|
|
|
|
|
| Example:
Into an isosceles triangle, whose base length is 16
cm and equal sides of
10
cm each, is inscribed and then
circumscribed a circle. Distance of their centers is? |
| Solution:
Given, a
= 16
cm
and b
= 10 cm.
d
= ? |
|
|
| Example:
Legs of a right triangle are, a
= 4 and b
= 3, length of the angle bisector at the vertex
A
is? |
| Solution:
Given, a
= 4
and b
= 3.
sa
= ? |
|
|
| Example:
The altitude of a triangle to the side a,
ha
= 2 at what distance from the side
a
should be drawn
a line parallel to a
such that it divides the triangle to two parts of equal areas. |
| Solution:
Given, ha
= 2 and Atrapezium
= Atrangle.
x
= ? |
|
|
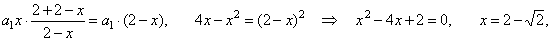 |
| Example:
Lengths of medians drawn from the vertices of acute angles of a right triangle are
7
cm and 4
cm. Length of the
hypotenuse is? |
| Solution:
Given, ma
= 7 cm
and mb
= 4 cm.
c
= ? |
|
|
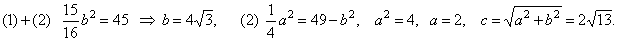 |
| Example:
Given is a triangle with sides,
b
= 6 cm, c
= 4 cm and the
median from the vertex
B, mb
= 5 cm, find the area of
the triangle. |
| Solution: Given,
b = 6,
c =
4 cm
and mb
= 5 cm.
AD
=
? Use of the cosine law. |
|
|
| Example:
Lengths of sides of a triangle are, a =
8 cm and b =
6 cm. How much is altitude
hb
to the side b greater than the
altitude ha
to the side a
if the length of the altitude ha =
4 cm? |
| Solution: Given,
a = 8 cm,
b = 6
cm and ha =
4 cm.
hb
-
ha =
? |
|
|
| Example:
The point of contact of incircle with radius 4
cm divides the side of a triangle to segments whose lengths are,
6
cm and 8
cm. The length of the biggest side of the triangle is? |
| Solution: Given,
r = 4 cm
and a
= 14 cm.
x
=
? |
|
|
|
|
| Example:
A side of a triangle |
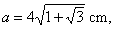 |
its angles,
b
= 30°
and g
= 45°, find the area of the |
|
| triangle. |
| Solution: Given,
side a,
b =
30° and g =
45°.
AD
=
? |
|
|
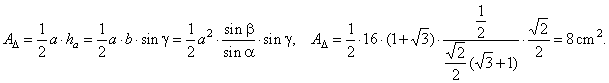 |
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |