|
| Geometry
- Triangle Problems and Solutions |
|
|
 Triangle, solved problems, examples
Triangle, solved problems, examples |
|
|
|
|
|
|
| Example:
Find the size of the angle that bisectors of the exterior angles on the hypotenuse of a right
triangle make. |
| Solution:
An angle supplementary to an angle of a
triangle is called an exterior angle of the triangle. |
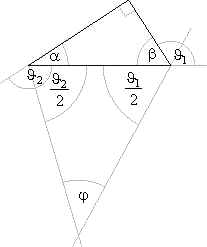 |
| The exterior angle is equal to the
sum of interior angles, not supplementary, |
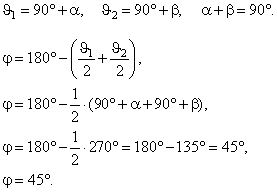 |
|
|
| Example:
Over the diameter of a circle of radius r
= 6 cm constructed is an equilateral triangle with the
side a =
12 cm, find the area of the part of the triangle outside the circle. |
| Solution:
Given, r
= 6 and a
= 12.
A
=
? |
|
|
| Example:
Find the biggest angle of a triangle with sides of, 5
cm, 4
cm and 2
cm. |
| Solution: Given,
a = 5,
b = 4 and
c = 2 .
a
=
?
Use of the cosine law. |
|
|
| Example:
The side of the square that is inscribed into an equilateral triangle with the side length 6 is? |
| Solution:
Given, a =
6.
x
=
? |
|
|
| Example:
Area of a triangle is 5
m2
the length of one side is 4
m and of other side
3 m, the sine of the
angle between given
sides is? |
| Solution:
Given,
A = 5
m2,
a = 4 m and b
= 3 m. sin
g
=
? |
|
|
| Example:
Sides of a triangle, a = 13,
b = 14 and
c
= 15, find the radius of the circle center of which lies on the side
c and
which touches sides, a and
b. |
| Solution:
Given, a = 13,
b = 14 and
c
= 15. r
=
? |
|
|
| Example:
To a circle of radius 30
cm, from a point distant
50
cm from the
circle center, drown are both tangents. Find the distance between
tangents. |
| Solution:
Given, r
= 30
cm and
OS
= 50
cm.
d(D1,
D2) = d = ? |
|
|
| Example:
Angles of a triangle ABC, which lay at the side
AB, are
70°
and 80°, if
O
is the intersection of altitudes of the
triangle and d =
angle (AOB) then, the sind is? |
| Solution:
Given, a
= 70°
and b
= 80°.
sin d = ? |
|
|
| Example:
Around a square with the side a
circumscribed is an equilateral triangle with the altitude h
and the
base coincident with the side of the square. Find the side of the equilateral triangle. |
| Solution:
Given, a
and h.
x = ? |
|
|
| Example:
In a right triangle the bisector of the angle a
divides opposite leg to two segments, find the ratio between greater
and smaller of segments. |
| Solution:
Given, a.
x
/ y = ? |
|
|
 |
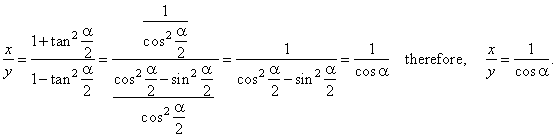 |
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |