|
| Trigonometry |
|
|
 Trigonometric
functions of arcs from 0
to ±
2p
Trigonometric
functions of arcs from 0
to ±
2p
|
|
Trigonometric
functions of arcs that differ on p/2 |
|
Trigonometric
functions of arcs that differ on p |
|
Trigonometric
functions of arcs whose
sum is
2p |
|
Trigonometric
functions of angles lying on axes |
|
|
|
|
|
|
|
|
|
Trigonometric
functions of arcs that differ on p/2
|
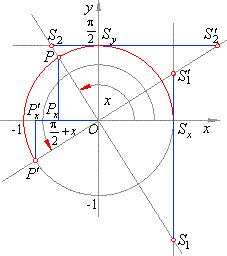
| Comparing the corresponding sides of the congruent right-angled triangles,
in the right figure, we get the relations of trigonometric functions of
an arc x and
the arc p/2
+ x |
| |
Px′P′
= OPx => |
sin
(p/2
+ x) = cos x
|
|
|
| |
OPx′
= -PxP
=> |
cos
(p/2
+ x) = -sin
x
|
|
|
| |
SxS1′
= -SyS2 => |
tan
(p/2
+ x) = -cot x
|
|
|
| |
SyS2′
= -SxS1 =>
|
cot
(p/2
+ x) = -tan x
|
|
|
|
 |
|
|
|
| Example:
Trigonometric functions of a given arc, angle or number should be expressed by the
corresponding function of angle which differ from the given for
90° (p/2).
|
|
|
|
a) sin
1,
b) cos 150°,
c) tan (-7p/4),
d) cot 50°.
|
| Solution:
a) sin
1 = -
cos (p/2
+ 1)
= -
cos 2.570796... |
|
b) cos 150°
= cos
(90°
+ 60°) = -
sin 60°
|
|
c) tan (-7p/4)
= -
cot (p/2
-
7p/4)
= -
cot ( -
5p/4)
= cot
(p
+ p/4) =
cot
p/4
|
|
d) cot 50°
= -
tan
(90°
+ 50°) = -
tan 140°.
|
|
|
|
Trigonometric
functions of arcs that differ on p
|
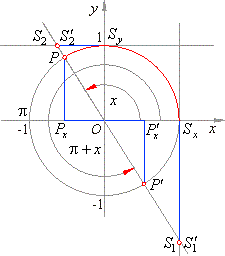
| Comparing the corresponding sides of the congruent right-angled |
| triangles,
in the right figure, we get the relations of trigonometric
|
| functions of
an arc x and
the arc p
+ x |
|
| |
Px′P′
= -
PxP
=> |
sin
(p
+ x) = -
sin
x
|
|
|
| |
OPx′
= -
OPx
=> |
cos
(p
+ x) = -
cos
x
|
|
|
| |
SxS1′
= SxS1 => |
tan
(p
+ x) = tan
x
|
|
|
| |
SyS2′
= SyS2 => |
cot
(p
+ x) = cot
x
|
|
|
|
 |
|
|
|
| Example:
Trigonometric functions of a given arc, angle or number should be expressed by the
corresponding function of angle which differ from the given for
180° (p).
|
|
a) sin
235°,
b) cos p/6,
c) tan (-300°),
d) cot 4.
|
| Solution:
a) sin
235°
= sin (180°
+ 55°) = -
sin 55°
|
|
b) cos p/6
= -
cos (p
+ p/6) =
-
cos
7p/6
|
|
c) tan (-300°)
= tan (180° -
300°) = tan (-120°)
= -
tan 120°
|
|
d) cot 4
= cot (p
+ 0.858407...) = cot 0.858407....
|
|
|
| Example:
Simplify expression
cot (p
-
x)
· cos
(p/2
+ x)
+ tan (p/2
-
x)
· tan
(p
+ x) -
cos (-
x)
|
| Solution:
cot (p
-
x)
· cos
(p/2
+ x)
+ tan (p/2
-
x)
· tan
(p
+ x) -
cos (-
x) = |
|
= -
cot x
· ( -
sin x)
+ cot x
· tan x
-
cos x = cos x
+ 1 -
cos x =
1.
|
|
|
|
Trigonometric
functions of arcs whose
sum is 2p
|
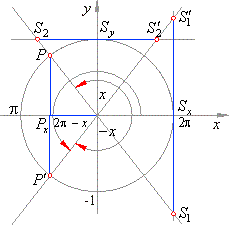
| The
right figure shows relations between sides of the congruent |
| right-angled triangles as
follows,
|
|
| |
PxP′
= -
PxP
=> |
sin
(2p
-
x) = -
sin
x
|
|
|
| OPx
= cos (2p
-
x)
= cos x |
cos
(2p
-
x) = cos
x
|
|
|
| |
SxS1′
= -
SxS1
=> |
tan
(2p
-
x) = -
tan
x
|
|
|
| |
SyS2′
= -
SyS2
=> |
cot
(2p
-
x) = -
cot
x
|
|
|
|
 |
|
|
|
| Example:
Trigonometric functions of a given arc, angle or number should be expressed by the
corresponding function of angle which when added with a given make
360° (2p).
|
|
a) sin
p/3,
b) cos 1,
c) tan 330°,
d) cot 10p/11.
|
| Solution:
a) sin
p/3
= -sin (2p
-
p/3) =
-
sin 5p/3 |
|
b) cos 1 = -
cos (2p
-
1) = cos 5.283185...
|
|
c) tan 330° =
tan (360° -
330°) = -
tan 30°
|
|
d) cot 10p/11
= -
cot (2p
-
10p/11) =
-
cot p/11.
|
|
|
| Example:
Prove that sin
320°
+ cos 50° = 0.
|
| Solution:
Since
sin 320° = sin (360°
-
40°) = -
sin 40°, and as
cos 50° = sin 40° |
|
then
-
sin 40°
+ sin
40° = 0.
|
|
|
|
Trigonometric
functions of angles lying on axes
|
|
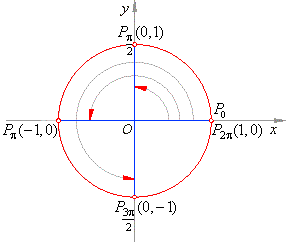
Values of trigonometric functions of characteristic arcs,
0,
p/2,
3p/2
and
2p
follow directly from the definitions.
|
|
|
Thus, for functions sine and
cosine from
the above figure we read the coordinates of the arc terminal point
P
that is, for the sine function we read the ordinate
while for the cosine function the abscissa of the terminal
point.
|
|
Therefore,
sin 0 = 0,
sin p/2
= 1,
sin p =
0,
sin 3p/2
= -1,
sin 2p
= 0,
|
|
and cos
0 = 1,
cos p/2 =
0,
cos p =
-1,
cos 3p/2 =
0,
cos 2p =
1.
|
|
|
|
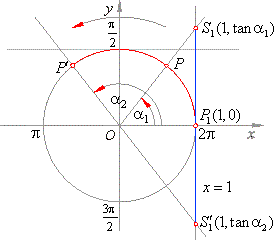
Point S1
whose ordinate determines the value of the
function tangent,
for the arcs,
0,
p
and 2p,
coincide with the initial point P1
of the arc, i.e., lies on the x-axis,
see the down figure.
|
|
|
Thus,
tan 0 = 0,
tan p
= 0,
tan 2p =
0,
|
|
while for arcs, p/2
and 3p/2
their terminal side or its extension lies on the y-axis, that is parallel with tangent
x =
1. There is no intersection S1
and we say that for these arcs the function tangent is
undefined.
|
|
However, if we follow the intersection point
S1 while the arc increases from
0
to p/2
we see that it moves away the x-axis and its
ordinate tan a1
tends to infinity (+
oo) which can be written as,
|
|
when a1
® p/2,
tan a1
®
+ oo
or tan
p/2
= oo .
|
|
If we continue to follow changes of the values of the function tangent, i.e., changes of the ordinates of the
intersection
S1′ while the arc increases from
p/2
to p that is, while the terminal side of the angle
a2
or its extension continue rotates in the positive direction, we see that point
S1′ moves toward the
x-axis and at the same time its ordinate
tan
a2 increases from
-
oo to
0.
|
|
Thus we can write, tan
p/2
= ± oo .
Examining the same way it follows that, tan
3p/2
= ± oo .
|
|
|
|
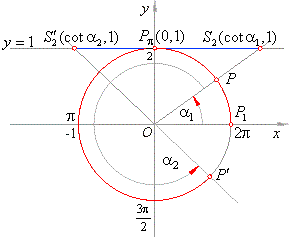
The intersection point S2,
whose abscissas determine the values of the function
cotangent, coincide with the point Pp/2 for the arcs
p/2
and 3p/2 on the
y-axis, so
|
|
cot p/2
= 0 and
cot 3p/2
= 0
|
|
while for arcs, 0(2p) and
p, the terminal side of the
corresponding central angle, or its extension, lies on the
x-axis
parallel with the tangent
y = 1, so there is no intersection
point.
|
|
We say that the function cotangent is undefined for those arcs.
|
|
|
To determine bounds of the values that the function cotangent
takes while the terminal point of an arc rounds the unit circle in the
positive direction passing through mentioned characteristic values,
0(2p) and
p, we should follow the intersection point
S2
on the tangent
y = 1, i.e., the changes of its abscissas
cot
a,
see
the above figure. Thus,
|
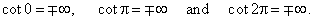
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Functions
contents B
|
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |