|
| Trigonometry |
|
|
|
Trigonometric
Functions |
 Periodicity of
trigonometric functions
Periodicity of
trigonometric functions |
 Signs of trigonometric
functions
Signs of trigonometric
functions |
|
The table of signs of trigonometric
functions |
|
|
|
|
|
|
| Periodicity of
trigonometric functions |
| After the argument (arc)
x
passes through all real values from the interval 0
< x < 2p or after the terminal side
of an angle turned round the origin for an entire circle, trigonometric or circular functions will repeat their
initial values. |
| As the terminal point
P
of an arc continue rotation around a unit circle in the positive direction passing over
the initial point P1 , it takes next values from the interval
2p
<
x < 4p, then the values from the interval 4p
< x < 6p and so on. |
| On the same way we can examine the rotation of the terminal point
P of an arc
x in the
negative (clockwise) direction, when it will pass through the values from the
intervals, 0 to
-2p, from
-2p
to -4p, and so on. |
| It follows that the argument
x can take any
value, |
| x
= arad
+ k · 2p,
k
= 0, ±1, ±2, ±3,
. . . or
x
= a°
+ k · 360°, k
Î
Z. |
| that is, every real value between
-
oo
and +
oo. |
| Particularly, for
k = 0, i.e., during the first rotation the value of
argument is x
= arad. |
| While the arc endpoint continues rounding over the starting point the trigonometric functions will, in
every interval of length
2p (i.e., from
2p to
4p, from
4p to
6p,
. . . , or from
0 to
-2p, from
-2p to
-4p,
. . . ) take the same values in the same order they took in the first interval
[0,
2p]. |
| Functions which have the characteristic to take the same values while their argument changes for all integral
multiples of a constant interval (or a constant increases in amount called increment) we call
periodic functions, and this constant interval we call
period. |
| Hence, we say that trigonometric functions are periodic functions of
x, so that |
|
f (x) = sin x
and f (x)
= cos x of
the period P
= 2p, |
| while
functions, f
(x)
= tan x
and f
(x)
= cot x of
the period P =
p. |
|
The periodicity of trigonometric functions show the
identities,
|
| |
sin
(a
+ k · 2p)
= sin a
and cos
(a
+ k · 2p)
= cos a,
k
Î Z |
|
|
| |
tan
(a
+ k · p)
= tan a
and cot
(a
+ k · p)
= cot a,
k
Î Z |
|
|
|
|
|
Signs of trigonometric
functions
|
|
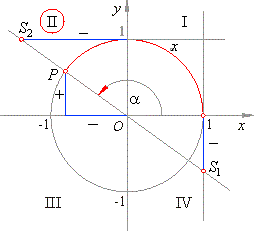
Quadrant I
- Values of trigonometric functions, sine, cosine, tangent and cotangent of any arc from
the first quadrant are all positive as positive are the coordinates of the points,
P,
S1
and S2
that define their values.
|
|
|
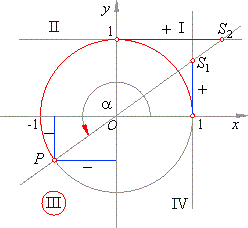
Quadrant II
- For arcs from the second quadrant points, P
and S2
both have negative abscissas (see the above figure), so the cosine and cotangent are negative. The ordinate of the terminal point
P
is positive so that the sine is positive while the ordinate of the point
S1
is negative, thus the tangent is negative.
|
|
|
Quadrant III
- As the abscissas and the ordinates of the terminal points P
of arcs from the third quadrant (see the above figure) are negative it follows that cosine and sine functions of these arcs are negative. The ordinates of the points
S1 and the abscissas of the points
S2 that belong to the arcs from the third quadrant are positive. Thus, the tangent and cotangent of these arcs are positive.
|
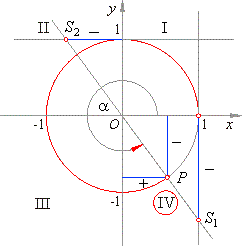
|
|
Quadrant IV
- The functions, sine, tangent and cotangent of the arcs from the fourth quadrant are negative as are the coordinates of the points,
P,
S1
and S2, that belong to them. Only the cosine function of arcs from the fourth quadrant is positive as are the abscissas of points
P that belong to them
(see the above figure).
|
|
|
|
The table of signs of trigonometric
functions
|

|
|
|
| Example:
To which quadrant belongs the endpoint of an arc
a
if
sin a < 0 and
cot a
> 0.
|
|
Solution: The
right figure shows that the ordinate of |
| the endpoint P
of an arc from the third quadrant is |
| negative, so sin
a < 0
while the abscissa of the
|
| point (in which the extension of the terminal side of |
| the angle
a
intersects the tangent y =
1) is positive, |
| i.e., cot
a
> 0.
|
| That is in accordance with the signs in the above
|
| table.
|
|
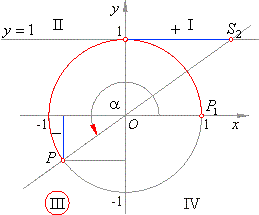 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Functions
contents B
|
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|