Unit of measurement of angles, Radian the circular measure, Protractor an instrument for measuring angles, Degrees to radians and radians to degrees conversion examples

Trigonometry

Trigonometric Functions

Unit of measurement of angles - a radian (the circular measure)

Protractor - an instrument for measuring angles

Degrees to radians and radians to degrees conversion examples

Unit of measurement of angles - a radian (the circular measure)

The relation between a central angle a (the angle between two radii) and the corresponding arc l in the circle of radius r is shown by the proportion,

a° : 360° = l : 2rp

It shows that the central angle a° compared to the round angle of 360°

(called perigon) is in the same relation as the corresponding arc l

compared to the circumference 2rp. Therefore,

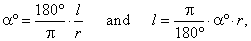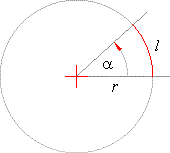where the ratio

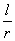we call the circular measure, usually denoted a^rad, i.e.,

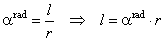thus,

The central angle subtended by the arc equal in length to the radius, i.e. l = r,

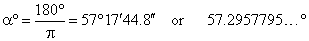we call it radian.

Thus, the angle a = 1° equals in radians,

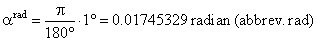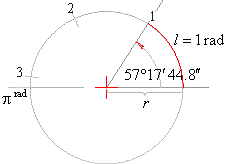or arc1° = 0.01745329. Arc is abbreviation from Latin arcus, (p = 3.1415926535...).

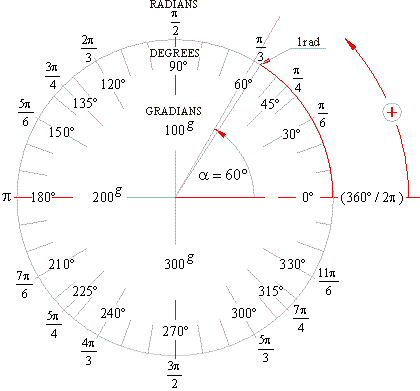
Protractor - an instrument for measuring angles

Mentioned relations between units of measurement of an angle and arc clearly shows the protractor shown in the below figure marked with radial lines indicating degrees, radians and rarely used gradians (the angle of an entire circle or round angle is 400 gradians).

A right angle equals 100 grad (gradians).

The hundredth part of a right angle is 1^g grad, and one 100th part of 1grad is centesimal arc minute 1^c, and one 100th part of centesimal arc minute is centesimal arc second 1^cc, therefore

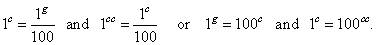Degrees to radians and radians to degrees conversion examples

Example: Convert 67°18´ 45" to radians.

Solution: The given angle we write in the expanded notation and calculate its decimal equivalent,

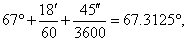then use the formula to convert degrees to radians

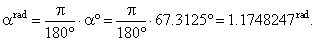Using a scientific calculator, the given conversion can be performed almost direct.

Before a calculation choose right angular measurement (DEG, RAD, GRAD) by pressing DRG key, then input, 67.1845 INV ®DEG 67.3125°

Because a calculator must use degrees divided into its decimal part one should press ®DEG (or ®DD) to get decimal degrees. Then press INV DRG® to get radians, 1.174824753^rad.

Example: Convert 2.785^rad to degrees, minutes and seconds.

Solution: Using formula,

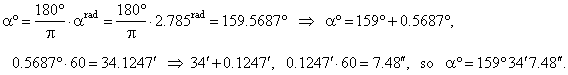The same result one obtains with a calculator through the procedure, press DRG key to set RAD measurement, then input 2.785 INV DRG® 177.2986066 grad = 177^g29^c86^cc, press again INV DRG® 159.5687459° obtained are decimal degrees (DEG), and to convert to degrees/minutes/seconds press INV ®DMS to get 159° 34´ 7.48".

Example: Find the length of the arc l that subtends the central angle a = 123°38´ 27" in the circle of radius r = 15 cm.

Solution: First express the angle a in decimal degrees, i.e.

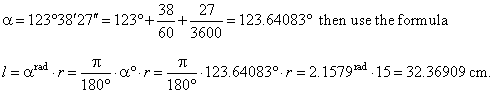Functions contents B