|
|
|
Rational
Functions |
 Basic
properties of rational functions
Basic
properties of rational functions |
 The
graph of the reciprocal
function, equilateral or rectangular hyperbola
The
graph of the reciprocal
function, equilateral or rectangular hyperbola |
 Translation of
the reciprocal function, linear rational function
Translation of
the reciprocal function, linear rational function |
|
|
|
|
|
|
|
Rational
Functions |
| ·
Rational functions - a ratio of two polynomials |
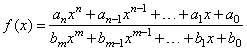 |
|
-
Reciprocal
function |
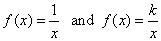 |
| |
-
Translation of the reciprocal function
or linear rational function. |
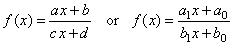 |
|
|
| Basic
properties of rational functions |
| Vertical,
horizontal and oblique or slant asymptotes |
| A
line whose distance from a curve decreases to zero as the
distance from the origin increases without the limit is called
the asymptote. |
| The
definition actually requires that an asymptote be the tangent to
the curve at infinity. Thus, the asymptote is a line that the
curve approaches but does not cross. |
| The
functions that most likely have vertical, horizontal and/or
slant asymptotes are rational functions. |
| So,
vertical asymptotes occur when the
denominator of the simplified rational function is equal to 0.
Note that the simplified rational function has cancelled all
factors common to both the numerator and denominator. |
| The
existence of the horizontal asymptote
is related to the degrees of both polynomials in the numerator
and the denominator of the given rational function. |
| Horizontal
asymptotes occur when either, the degree of the numerator is
less then or equal to the degree of the denominator. |
In
the case when the degree (n)
of the numerator is less then the degree (m)
of the denominator, the x-axis
y = 0
is the asymptote. |
| If
the degrees of both polynomials, in the numerator and the
denominator, are equal then, y
= an/bm
is the horizontal asymptote, written as the ratio of their
highest degree term coefficients respectively. |
| When
the degree of the numerator of a rational function is greater
than the degree of the denominator, the function has no
horizontal asymptote. |
| A
rational function will
have a slant (oblique) asymptote
if the
degree (n)
of the numerator is exactly one more than the degree (m)
of
the denominator that is if n
= m + 1. |
| The
graph of a rational function will never cross its vertical
asymptote, but may cross its
horizontal or slant asymptote. |
|
| The
graph of the reciprocal
function, equilateral or rectangular hyperbola |
| The
graph of the reciprocal function y
= 1/x or y
= k/x is a
rectangular (or right) hyperbola of which asymptotes are the
coordinate axes. |
| If
k
> 0 then,
the function is decreasing from zero to negative
infinity and from positive infinity to zero,
i.e., the graph of the rectangular hyperbola has
two branches, in the first and third quadrants as is
shown in the right figure. |
| The
hyperbola has two axes of symmetry. |
| The
vertices, |
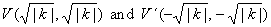 |
|
|
|
 |
|
|
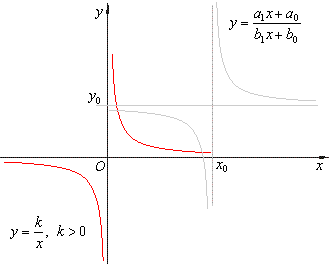
| Translation
of the reciprocal function, linear rational function |
| The
rational function |
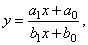 |
by
dividing the numerator by denominator, |
|
| can
be rewritten into |
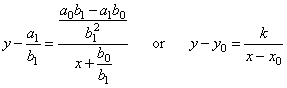 |
where, |
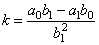 |
|
| is
the constant, |
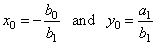 |
are
the vertical and the horizontal asymptote respectively. |
|
| Therefore,
the values of the vertical and the horizontal asymptotes
correspond to the coordinates of the horizontal and the vertical
translation of the reciprocal function y
= k/x as is
shown in the figure below. |
 |
|
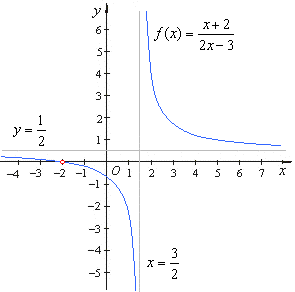
| Example: Given
the rational function |
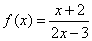 |
sketch
its graph. |
|
| Solution:
The
vertical and the horizontal asymptote of the linear rational
function |
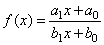 |
|
|
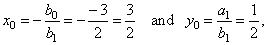 |
| and the
coefficient |
 |
 |
| The
x-intercept
at a point (x,
0), |
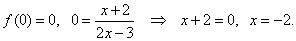 |
| The
y-intercept
at a point (0,
y), |
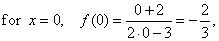 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents C |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |