|
|
| Polynomial and/or Polynomial
Functions and Equations |
The general form
or translatable form of the polynomial |
|
The
coordinates of translations and the coefficients of the source
function formulas |
|
Quadratic
function formulas |
|
Cubic function formulas |
|
Quartic
function formulas |
|
Quintic
function formulas |
|
Sextic function formulas |
|
|
|
|
|
|
| The general form
or translatable form of the polynomial |
| The
coordinates of translations and the coefficients of the source
function formulas |
| Therefore,
every given polynomial written in the general form can be
transformed into translatable form by calculating the
coordinates of translations x0
and y0 and the coefficients a
of its source function. |
|
Thus, for n
= 2, quadratic
y
=
a2x2
+
a1x + a0
or y
-
y0
=
a2(x
-
x0)2,
where
|
|
|
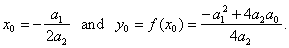
by setting
x0
=
0
and y0
=
0,
y
=
a2x2
- the source quadratic.
|
|
|
|
For n
= 3, cubic function
y
=
a3x3
+
a2x2
+
a1x + a0
or y
-
y0
=
a3(x
-
x0)3
+
a1(x
-
x0),
|
|
by setting
x0
=
0
and y0
=
0,
y
=
a3x3
+ a1x
- the source cubic function, where
|
|
|
|
|
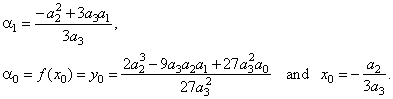
For n
= 4, quartic
function
y
=
a4x4
+ a3x3
+
a2x2
+
a1x + a0
|
|
or y
-
y0
= a4(x
-
x0)4
+
a2(x
-
x0)2
+
a1(x
-
x0),
|
|
by setting
x0
=
0
and y0
=
0,
y
=
a4x4
+ a2x2
+ a1x
- the source quartic function, where
|
|
|
|
|
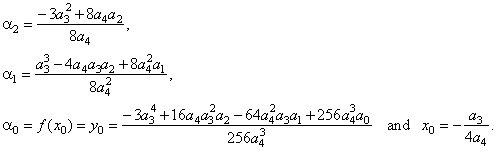
For n
= 5, quintic
function
y
=
a5x5
+
a4x4
+ a3x3
+
a2x2
+
a1x + a0
|
|
or y
-
y0
= a5(x
-
x0)5
+
a3(x
-
x0)3
+
a2(x
-
x0)2
+
a1(x
-
x0),
|
|
by setting
x0
=
0
and y0
=
0,
y
=
a5x5
+ a3x3
+ a2x2
+ a1x
- the source quintic function, where
|
|
|
|
|
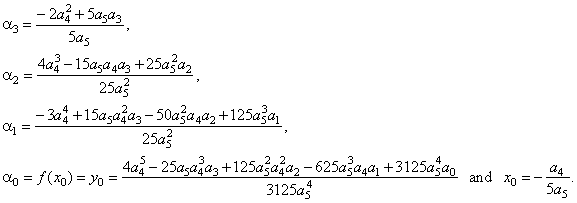
For n
= 6, sextic
function
y
=
a6x6
+
a5x5
+
a4x4
+ a3x3
+
a2x2
+
a1x + a0
|
|
or y
-
y0
= a6(x
-
x0)6
+
a4(x
-
x0)4
+
a3(x
-
x0)3
+
a2(x
-
x0)2
+
a1(x
-
x0),
|
|
by setting
x0
=
0
and y0
=
0,
y
=
a6x6
+ a4x4
+ a3x3
+ a2x2
+ a1x
- the source sextic, where
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents C |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
