|
|
| Polynomial and/or Polynomial
Functions and Equations |
 Polynomial functions
Polynomial functions |
|
The source or the original polynomial function |
|
Translating
(parallel shifting) of the source polynomial function |
|
Coordinates of translations and their role in the polynomial
expression |
 Roots or zeros of
polynomial function
Roots or zeros of
polynomial function |
|
|
|
|
|
|
| Polynomial functions |
| The
source
or the original polynomial function |
| A
polynomial f
(x)
= anxn
+ an-1xn-1
+ .
. . +
a1x
+ a0
of degree n ³
1, consisting
of n
+ 1 terms, shown graphically, represents translation of its
source (original) function in the direction of the coordinate
axes. |
|
The complete source polynomial function |
|
fs(x)
= anxn
+ an-2xn-2
+ .
. . +
a2x2
+ a1x
|
|
|
| has
n
- 1 terms
lacking second and the constant term, since its coefficients, an-1
=
0
and a0
=
0
while
the leading coefficient an,
remains unchanged. |
| Therefore,
the source polynomial function passes through the
origin. |
| A
coefficient ai
of
the source function is expressed by the coefficients of the general
form. |
| A
coefficient ai
of
the source polynomial can be calculated like
coefficients of the Taylor polynomial |
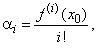 |
| where
f (i
)
(x0)
denotes i-th derivative at
x0. |
|
| Translating
(parallel shifting) of the source polynomial function |
| Thus,
to obtain the graph of a given polynomial function f
(x)
we translate (parallel shift)
the
graph of its source function in the direction of the x-axis
by x0
and in the direction of the y-axis
by y0. |
| Inversely,
to put a given graph of the polynomial function beck to the
origin, we translate it in the opposite direction, by taking the
values of the
coordinates of translations with opposite sign. |
|
| Coordinates of translations
and their role in the polynomial expression |
| The
coordinates of translations we calculate using the formulas, |
|
|
| Therefore,
by plugging the coordinates of translations into
the source polynomial function fs(x),
i.e., |
|
y
- y0
= an(x
- x0)n
+ an-2(x
- x0)n-2
+ .
. . +
a2(x
- x0)2
+ a1(x
- x0) |
|
|
| and
by expanding above expression we get the polynomial function in
the general form. |
|
| Inversely, by plugging the coordinates of translations into a given polynomial function
f(x), that is expressed in the general form,
i.e., |
|
y
+ y0
= an(x
+ x0)n
+ an-1(x
+ x0)n-1
+ .
. . + a1(x
+ x0)
+ a0 |
|
|
| and
after expanding and reducing above expression we get its source polynomial function. |
| Note
that in the above expression the signs of
the coordinates of translations are already changed. |
| Therefore,
each polynomial missing second term (an-1
=
0),
represents a source polynomial whose graph is translated in
the direction of the y-axis
by y0
= a0. |
|
| Roots or zeros of
polynomial function |
| The
zeros of a polynomial function are the values of x
for which the function equals zero. |
| That
is, the solutions of the equation f
(x)
= 0,
that are called roots of the polynomial, are the zeros of the
polynomial function or the x-intercepts of its
graph in a coordinate plane. |
| At
these points the graph of the polynomial function cuts or
touches the x-axis. |
| If
the graph of a polynomial intersects with the x-axis
at (r,
0), or x
= r
is a root or zero of a polynomial, then |
| (x
-
r)
is a factor of that polynomial.
|
| Every
polynomial of degree n
has exactly n
real and/or complex zeros. |
| An
nth
degree polynomial has at most n
real zeros. |
| Some
of the roots may be repeated. The number of times a root is
repeated is called multiplicity or
order of the root. |
| The
number ri
is a root of the
polynomial f
(x)
if and only if
f (x)
is divisible by
(x
-
ri).
|
| Therefore,
a polynomial and/or polynomial
function with
real coefficients can be expressed as a product of its leading
coefficient an
and
n
linear factors of the form (x
- ri),
where ri
denotes its real root and/or complex root, |
| f
(x)
= anxn
+ an-1xn-1
+
.
. . +
a1x
+ a0
= an(x
- r1)(x
- r2)
.
. . (x
- rn).
|
| Thus, finding the roots of a
polynomial f(x)
is equivalent to finding its
linear divisors or is equivalent to polynomial
factorization into
linear factors. |
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents C |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |