|
|
Parametric Equations |
 The parametric equations of a
circle
The parametric equations of a
circle
|
|
The parametric equations of a
circle
centered at the origin with radius
r |
|
The parametric equations of a
translated circle with center (x0, y0) and radius r |
 The parametric equations of an
ellipse
The parametric equations of an
ellipse |
|
The parametric equations of an
ellipse
centered at the origin |
|
The parametric equations of a
translated ellipse with center at (x0, y0) |
|
|
|
|
|
|
|
| The parametric equations of a
circle
|
| The parametric equations of a
circle
centered at the origin with radius r |
| The parametric equations
of a
circle
centered at the origin |
| with radius
r, |
|
|
| where, 0
< t < 2p. |
| To
convert the above equations into Cartesian
coordinates, |
| square
and add both equations, so we get |
| x2
+ y2
= r2 |
| as sin2
t
+ cos2
t = 1. |
|
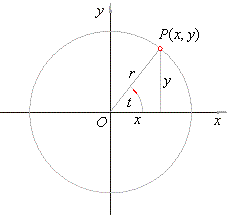 |
|
|
| The parametric equations of a
translated circle with center (x0, y0) and radius r |
| The parametric equations
of a
circle with center |
| (x0,
y0)
and
radius r, |
| x
= x0
+ r cos t |
| y
= y0
+ r sin t |
|
|
| where, 0
< t < 2p. |
| If
we write
the above equations, |
|
x
- x0
= r cos t |
| y
- y0
= r sin t |
| then
square and add them we get the
equation |
| of the
translated circle in Cartesian coordinates, |
| (x
- x0)2
+
(y
- y0)2
= r2. |
|
 |
|
|
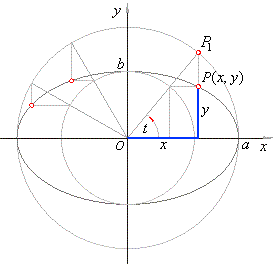
| The parametric equations of an
ellipse |
| The parametric equations of an ellipse
centered at the origin |
| Recall
the construction of a point of an ellipse using two concentric circles of radii equal to lengths of the |
| semi-axes a and b, with the center at the origin as shows |
| the
figure,
then |
|
|
| where, 0
< t < 2p. |
| To
convert the above parametric equations into Cartesian |
|
coordinates, divide the first
equation by
a
and the second |
| by b, then square and add them, |
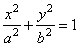 |
| thus,
obtained is the standard equation of the ellipse. |
|
 |
|
|
| The parametric equations of a
translated
ellipse with center at (x0, y0) |
| The parametric equations
of a translated ellipse with
center (x0,
y0)
and semi-axes a and b, |
| |
| x
= x0
+ a cos t |
| y
= y0
+ b sin t |
|
|
|
| To
convert the above parametric equations into Cartesian
coordinates, we write them as |
| |
| x
- x0
= a cos t |
| y
- y0
= b sin t |
|
|
|
| and divide the first
equation by
a
and the second by b, then square and add
both equations, so we get |
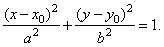 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Functions
contents B
|
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |