|
|
Parametric Equations |
 Parametric equations of a hyperbola
Parametric equations of a hyperbola
|
|
The
parametric equations of a hyperbola expressed by trigonometric functions |
|
The
parametric equations of a hyperbola expressed by hyperbolic
functions |
|
The
definition of the hyperbolic functions |
|
Relations
between hyperbolic and trigonometric or circular functions |
|
The
parametric equations of the equilateral or rectangular hyperbola |
|
The
parametric equations of the general hyperbola |
|
|
|
|
|
|
|
| Parametric equations of a hyperbola
|
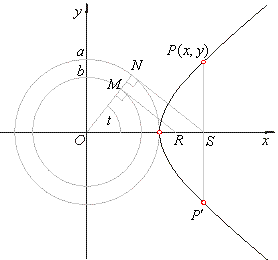
| In the construction of the hyperbola, shown in
the figure below, circles of radii
a
and b
are intersected by an
arbitrary line through the origin at points
M
and N.
|
| Tangents to the circles at
M
and N
intersect the x-axis at
R
and S.
|
|
On the perpendicular to the x-axis
through S
mark the line segment
SP of
the length
MR to get the point
P
of the hyperbola.
|
| Let
prove that P is a point of the hyperbola.
|
|
In the right
triangles ONS and
OMR,
|
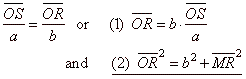
|
|
by replacing OS
= x
and MR
= SP
= y
|
|
and substituting |
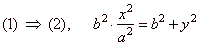 |
|
| by
dividing by b2, |
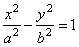 |
|
|
therefore, P(x, y)
is
the point of the hyperbola.
|
|
 |
|
| The coordinates of the point
P(x, y)
can also be expressed by the angle t
common to both triangles ONS and
OMR,
therefore |
|
|
| are the
parametric equations of the
hyperbola expressed by trigonometric functions. |
| By substituting these parametrically expressed coordinates into equation of the hyperbola |
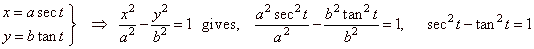 |
| that
is, known
trigonometric identity. |
|
| The
parametric equations of a hyperbola expressed by hyperbolic
functions |
| The
definition of the hyperbolic functions |
| The
hyperbolic functions are defined in terms of exponential functions
ex
and e-x
as
|
| |
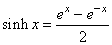 |
-hyperbolic sine,
|
|
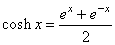 |
-hyperbolic cosine,
|
|
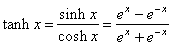 |
-hyperbolic
tangent,
|
|
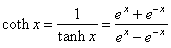 |
-hyperbolic
cotangent,
|
|
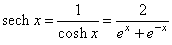 |
-hyperbolic
secant and |
 |
-
hyperbolic cosecant. |
|
| By
adding and subtracting formulas for the sinh
x and the cosh
x, we
get |
| cosh
x + sinh x = ex |
| cosh
x -
sinh x = e-x, |
| then
multiplying the two equations obtained is |
|
|
| the
basic identity of the
hyperbolic functions. |
|
| Relations
between hyperbolic and trigonometric or circular functions |
| Let
compare the basic identity of the hyperbolic functions with the
trigonometric identity obtained from the parametric
equations of the hyperbola expressed by trigonometric functions shown
above, |
| cosh2
x -
sinh2 x = 1 |
| sec2
a
-
tan2 a = 1 |
| therefore,
we can write |
| cosh
x = sec a
and sinh
x = tan a |
| by
substituting into |
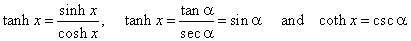 |
|
| The
parametric equations of the equilateral or rectangular hyperbola |
| The parametric equations |
|
|
| describe the right branch of the
rectangular hyperbola, |
| with semi-axes a
= b = 1
centered at the origin, while |
| the parameter t passes through all real values
from |
| -
oo to + oo
. |
| Thus,
by squaring both equations then, subtracting the |
| second
equation from the first and applying the basic |
| identity,
obtained is |
| x2
-
y2
= 1 the rectangular hyperbola. |
|
 |
|
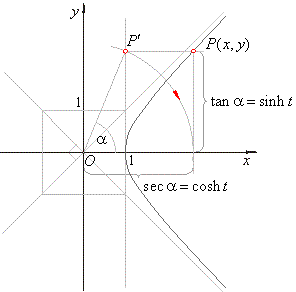
| The
above figure shows the construction of a point P(x,
y)
of the rectangular hyperbola using the relations between
hyperbolic and trigonometric functions. |
| Use
the hypotenuse of the right triangle O1P'
and the side opposite to the angle a
to get the abscissa and the
ordinate of a point of the hyperbola respectively, as |
| x = sec a =
cosh
t and y
= tan a =
sinh t. |
| By
changing values of the angle a
from the interval -
p/2
< a
< p/2
we can get every point of the |
| hyperbola. |
|
| The
parametric equations of the general hyperbola |
| The parametric equations |
| |
| x
= a cosh
t |
| y
= b sinh t, |
|
-
oo
< t
< + oo |
|
| represent
the general hyperbola since plugging the coordinates x
and y
into the equation of the hyperbola |
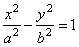 |
| yield
the basic identity cosh2
x -
sinh2 x = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Functions
contents B
|
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |