|
|
|
Absolute value
functions and equations |
 The graph of the
absolute value function f (x)
= |
x
|
The graph of the
absolute value function f (x)
= |
x
| |
 The graph of absolute value of
a linear function f (x) =
| ax+
b |
The graph of absolute value of
a linear function f (x) =
| ax+
b |
|
 Linear equation with
absolute value, graphic solution
Linear equation with
absolute value, graphic solution |
|
|
|
|
|
|
| Absolute
value functions
and equations |
| The
graph of the absolute
value function f (x)
= |
x
| |
| The
definition for the absolute value of a function is given by |
|
|
| Thus,
for
values of x
for which f (x)
is nonnegative, the graph of | f (x)| is the
same as that of f (x).
|
| For values of
x
for which f (x)
is
negative, the graph of | f(x)
| is a reflection of
the graph of f (x)
on the x
axis. |
| That
is, the
graph of y = -
f (x) is obtained by reflecting the graph
of y = f (x)
across the x-axis. |
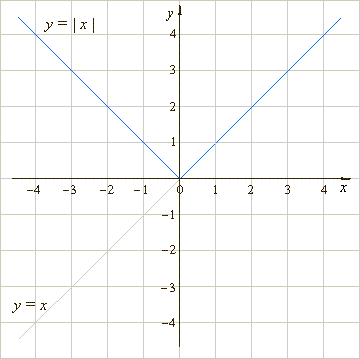
| Hence,
the graph of the absolute value of
the function
f (x) =
x,
i.e.,
| x | is |
 |
|
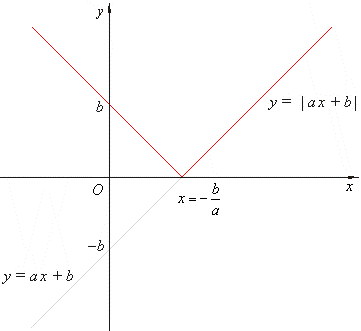
| The
graph of the absolute value of a linear
function f (x) =
| ax+
b |
|
 |
|
| Linear equation with
absolute value, graphic solution |
| Recall
that the absolute value of a real number a,
denoted |a|,
is the number without its
sign and represents the distance between 0 (the origin) and that
number on the real number line. |
|
Thus, regardless of the value of a number
a
its absolute value is
always either positive or zero, never negative that is, |
a | > 0.
|
| To
solve an absolute value equation, isolate the absolute value on
one side of the equation, and use the definition of absolute
value. |
| If the number on the other side of the equal sign is positive, we will need to set up two
equations to get rid of the absolute value, |
|
- the first equation that set the expression inside the absolute value symbol equal to the other side of the equation, |
|
- and the second equation that set the expression inside the absolute value equal to the
opposite of the number on the other side of the equation. |
| Solve
the two equations and verify solutions by plugging the solutions
into the original equation. |
| If
the number on the other side of the absolute value equation is negative then
the equation has no solution. |
|
|
Example:
|
-3
- x
| = 2
|
|
Solution: |
|
| -3
-
x = 2 or
-3
-
x = -2 |
|
x = -
5
x = -1 |
|
| The
solutions to the given equation are |
|
x = - 5
and x = -1. |
|
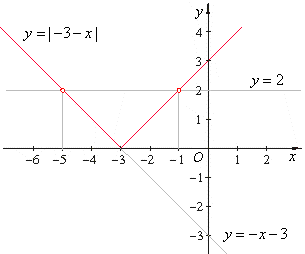 |
|
| |
|
Example:
|
x + 1 | =
2x -
3
|
|
Solution:
x + 1 = 2x
-
3
or
x + 1 = -(2
x -
3) |
|
x - 2x
= - 4
x +
2x = 3 -
1 |
|
x = 4
3x = 2
=> x = 2/3 |
|
| Check
solutions: |
| x = 4
=>
|
x + 1 | =
2x -
3,
x = 2/3
=>
|
x + 1 | =
2x -
3 |
|
|
4
+ 1 | =
2 · 4 -
3
|
2/3 + 1 | =
2 · 2/3 -
3
|
|
5 = 5
5/3 is not
-5/3 |
|
| The
check shows that x =
2/3 is not a solution,
because the right side of the equation becomes negative. There is a single solution to this equation: x = 4. |
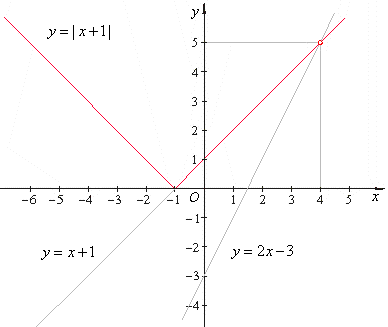 |
|
|
Example:
|
x + 2 | =
| 2x -
5 |
|
|
Solution: As both
sides of the equation contain absolute values the
only way the two sides are equal is, the two quantities
inside the absolute value bars are equal or equal but with
opposite signs.
|
|
x + 2 = 2x
-
5
or
x + 2 = -(2
x -
5) |
|
x -
2x
= -
5 -
2
x + 2 = -2
x +
5 |
|
-x =
-7
3x = 3 |
|
x = 7
x = 1 |
|
| Check
solutions: |
| x =
7 =>
|
x + 2 | =
| 2x -
5 |, x = 1
=>
|
x + 2 | =
| 2x -
5 | |
|
|
7 + 2 | =
| 2 · 7 -
5
|
|
1 + 2 | = | 2 ·
1 -
5 |
|
|
9 = 9
3 = | -3 | |
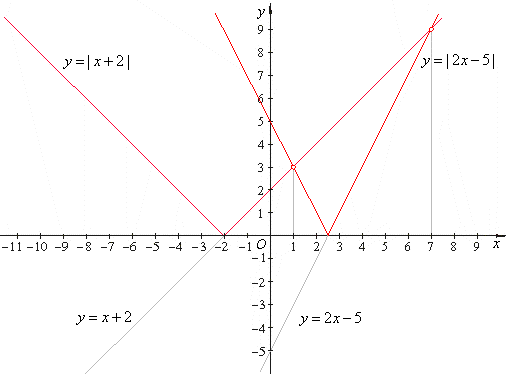 |
| Therefore,
the
solutions to the given equation are x =
1 and x =
7. |
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents C |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |