|
|
|
|
|
Sequences
and limits |
 Infinite
sequences
Infinite
sequences |
| Sequences notation -
the
rule for the n-th
term of a sequence |
|
Graphing the terms of a sequence on the number line |
 The limit of a sequence
The limit of a sequence |
|
The definition of the limit of a sequence |
|
Convergence of a sequence |
|
Verifying the convergence of a sequence from the definition, examples |
|
|
|
|
|
|
| Infinite
Sequences |
| An
infinite sequence is an ordered list of real numbers indexed by the
natural numbers n
Î
N
denoted {an} |
| a1,
a2, a3, . . . , an,
. . .
|
| where
by an
given is a rule to calculate the nth
term of the sequence. |
|
|
Graphing the terms of a sequence
on the number line |
| Thus,
for example; |
| (1)
an
= n
for n =
1, 2, 3,. . . gives the sequence,
1, 2, 3, 4, 5,.
. . |
| shown
on the number line |
 |
|
| (2) |
|
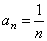 |
|
for n =
1, 2, 3,. . . gives the sequence, |
|
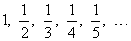 |
|
|
| shown
on the number line |
 |
|
| (3) |
|
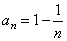 |
|
for n =
1, 2, 3,. . . gives the sequence, |
|
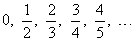 |
|
|
| shown
on the number line |
 |
|
| (4) |
|
 |
|
for n =
1, 2, 3,. . . gives the sequence, |
|
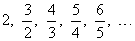 |
|
|
| shown
on the number line |
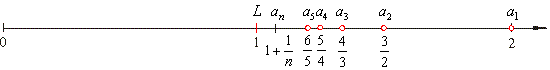 |
|
| (5) |
|
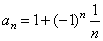 |
|
for n =
1, 2, 3, . . . gives the sequence, |
|
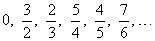 |
|
|
| shown
on the number line |
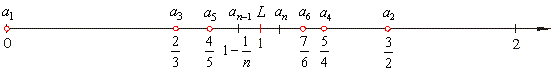 |
| Observe that, the first and the third sequence shown above both increase, the second and the fourth decrease,
and that the
terms of the fifth sequence oscillate (alternate) from the left to the right approaching closer and
closer to 1. |
|
| The limit of a sequence |
|
The definition of the limit of a
sequence |
| A
number L is
called the limit of a sequence {an}
if
for every positive number e there exist a natural number |
| n0
such that if n
> n0,
then |
an
-
L
|
< e. |
| That
is, a
number L is the limit of a sequence
if the distance between the term an
and L
becomes arbitrary small
by choosing n
large enough (see the examples above). The n0
denotes the value of the index n
starting from which the distance an
-
L
becomes smaller than the given e. |
|
Since the value of n0
depends on the size of e
it is usually written as n0(e). |
|
|
Convergence of a sequence |
| Therefore,
if a sequence {an}
has a limit L
we write |
| |
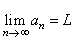 |
or |
an
®
L
as n
®
oo
|
|
|
| and
we say that that a sequence an
has the limit L
as n
tends to infinity. |
| A
sequence {an}
is
convergent if it has a limit. Otherwise, we
say the sequence is divergent. |
| Thus,
the sequences, (3),
(4)
and (5),
from the example above, all converge or tend to the limit 1. |
|
| Example: Let
examine the limit of the sequence (3)
given by |
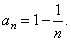 |
|
|
| Solution:
Prove that |
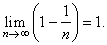 |
|
|
| The
sequence |
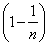 |
tends
to the limit 1
as the distance |
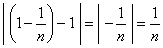 |
can
become |
|
| arbitrary small by
choosing the natural number n
sufficiently large. |
| For
example, if we choose
n = 100
the distance between an
and 1
is 1/n
= 0.01
that is, |
| for
all n > 100
the distance | an
-
1 | < 0.01. |
| Therefore,
n0(e)
= 101 meaning, starting from the 101st
term further, the distance of the remaining terms of the
sequence and 1,
is always less than 0.01. |
|
| Verifying
the convergence of a sequence from the definition examples |
| Example: Find
the limit of the sequence (2)
given by |
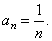 |
|
|
| Solution:
Let
prove that |
 |
|
|
| Using
the definition of limit we must find a natural number n0(e)
such that | an
-
0 | < e
for all n >
n0. |
| Therefore,
if n >
n0 then
|1/n -
0 | = |1/n | = 1/n < 1/n0 < e. |
| Suppose
we wish to make the difference (or the distance) between the anth
term and
the limit L
to be less than e
= 0.001 = 1/1000. |
| Then,
as 1/n < e
or n
> 1/e
it follows n
> 1000
that is, starting from n0
= 1001
the distance an
-
L becomes smaller than the given e. |
| Observe
that the absolute value of terms of the sequences that converge to zero
become arbitrary small as n
tends
to infinity that is,
| an
| < e
for all n >
n0(e). |
| For
example such sequences are, |
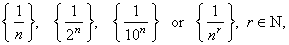 |
therefore |
|
|
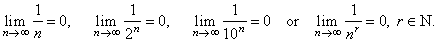 |
|
| The
same way we can prove that the sequence (5)
above,
given by |
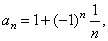 |
converges
to 1. |
|
| As
can be seen on the number line above, the
terms of the sequence alternate from left to right approaching closer and closer to
1 as n
tends
to infinity. |
| That
is, the sequence |
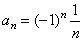 |
alone alternately converges from left to right approaching closer and |
|
| closer to 0 as
n
tends to infinity. |
|
|
Example: Find
the limit of the sequence,
0.9, 0.99, 0.999, . . . , 0.999
. . . 9 . . . , .
. .
|
|
Solution: The
terms of the sequence can be written as
|
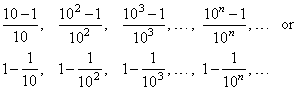 |
| Therefore,
|
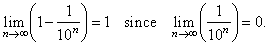 |
|
|
|
|
Example:
The
sequence
|
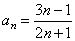 |
has
the limit
3/2,
starting
from which term |
an -
L | < 0.01.
|
|
|
|
Solution: Substitute
given values into the inequality |
an -
L
| < 0.01,
|
|
|
|
Check the result by plugging
n0(e)
= 125
into |
an -
L | < 0.01.
|
|