|
|
|
Introduction
to Functions |
 Function definition, notation and
terminology
Function definition, notation and
terminology |
|
Domain, range and
codomain |
|
Evaluating
a function |
|
Composition
of functions (a function of a function) |
|
Inverse
function
|
|
|
|
|
|
|
|
| Introduction
to Functions |
| Function definition, notation and
terminology |
|
A function
f
is
a relation between two sets, called the domain
and the range,
such that to each element x of the domain, there is assigned
exactly one element ƒ
(x) of the range. |
|
We also say that
a
function is an expression or a rule that associates
each element of the domain with a unique element
of the codomain. |
|
In
the function notation y = ƒ
(x),
x
is the independent variable or argument and y
is the dependent variable or a function of the variable x,
where f
is a rule of association. |
|
In the notation y = ƒ
(x)
we call y
the value of f
at x. |
|
Thus, ƒ
represents all the operations which should be performed to
evaluate the function at a particular value. |
|
|
|
Domain, range and
codomain |
|
The domain is
the set of values of the independent variable of a given function,
i.e., the set of all first members of the ordered pairs (x,
ƒ (x))
that
constitute the function. |
|
The range is
the set of values that given function takes as its argument varies
through its domain. It is the image of the domain. |
|
The codomain
is the set within which the values of a function lie, as opposed to
the range, which is the set of values that the function actually
takes. |
|
Therefore, the range must be a subset of,
but may or may not be identical with the codomain. |
|
We will only consider real-valued
functions of a real variable. |
|
|
| Evaluating
a function |
| Evaluating
a function means finding
ƒ
(x)
at some
specific value of x.
So, evaluating a function at a constant or a variable involves substituting the constant
or the variable into the expression of the function and
calculate its value. |
|
| Example: Given
ƒ(x)
= -x2 +
4x - 1
find, a) ƒ(-1) and
b) ƒ(x
+ 2). |
| Solution:
a)
ƒ(-1)
= -(-1)2 +
4(-1)
- 1
= -1
-
4 - 1
= -6 |
|
b) ƒ(x
+ 2)
= -(x
+ 2)2 +
4(x + 2) - 1
= -(x2 +
4x +
4) +
4x + 8 - 1
= -x2 + 3 |
|
| Composition
of functions (a function of a function) |
| Evaluation
of a function at the value of another (or the same) function is
called the composition of functions, denoted as (ƒ
o
g) (x) = ƒ (g (x)). |
| Thus,
the composition is the operation that forms a single function
from two given functions by plugging the second function into
the first for any argument. |
| The composition
of functions is only defined if the range of the first is
contained in the domain of the second function. |
|
| Examples: Given
ƒ
(x)
= -x2 +
4x - 1
and g (x)
= -x
+ 1
find; |
|
a) ƒ (g
(x)),
b) g (ƒ
(x)),
c) g (g
(x))
and d) ƒ
(g (-1)). |
|
| Solutions:
a) ƒ(g(x))
= ƒ(-x
+ 1)
= -(-x
+ 1)2 +
4(-x
+ 1)
- 1
= -x2
-
2x + 2 |
|
b) g(ƒ(x))
= g(-x2 +
4x - 1)
= -(-x2 +
4x - 1)
+ 1
= x2 -
4x + 2 |
|
c) g(g(x))
= g(-x
+ 1)
= -(-x
+ 1)
+ 1
= x |
|
d) ƒ(g(-1))
= ƒ( -(-1)
+ 1)
= ƒ(2)
= -22
+ 4 · 2 - 1
= 3 |
|
| Inverse
function
|
| The inverse function, usually written
f -1, is the function whose
domain and the range are respectively the range and domain of a given function
f, that is |
| f
-1(x)
= y if and only if
ƒ (y)
= x . |
| Thus, the
composition of the inverse function and the given function returns
x, which is called the
identity function, i.e., |
| f
-1(ƒ
(x))
= x and
ƒ (f
-1(x))
= x. |
| The inverse of a function undoes the procedure
(or function) of the given function. |
| A pair of inverse functions is in
inverse relation. |
| Example: If
given
ƒ (x)
= log2 x
then f -1(x)
= 2x
since, |
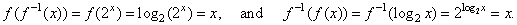 |
|
| Therefore,
to obtain the inverse of a function y = ƒ
(x), exchange the variables
x
and y,
i.e., write x = ƒ(y)
and solve for y.
Or form the composition ƒ(f
-1(x))
= x and solve
for f -1. |
|
| Example: Given
y = ƒ(x)
= log2 x form
f -1(x). |
| Solution:
a) Rewrite
y = ƒ
(x)
= log2 x
to x =
log2 y
and solve for y,
which gives y =
f
-1(x)
= 2x. |
|
b) Form ƒ
(f
-1(x))
= x that
is, log2
(f -1(x))
= x and
solve for f -1, which
gives f -1(x)
= 2x. |
|
| The
graphs of a pair of inverse functions are symmetrical with
respect to the line
y
= x. |
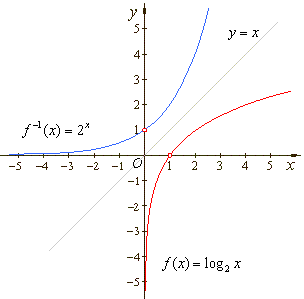 |
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents C |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |