|
|
|
|
Imaginary
and Complex Numbers |
 Exponentiation
and root extraction of complex numbers in the polar form
Exponentiation
and root extraction of complex numbers in the polar form |
|
Exponentiation
and root extraction of complex numbers examples
|
|
Powers and roots of
complex numbers, use of de Moivre’s formulas |
|
|
|
|
|
|
| Exponentiation
and root extraction of complex numbers in the polar form - de
Moivre's formula |
| We use the polar form
for exponentiation and root extraction of complex numbers that
are known as de Moivre's formulas. |
| |
zn
= rn · [cos(nj)
+ isin(nj)] |
|
|
| and |
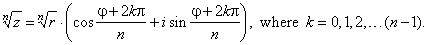 |
|
|
|
|
Exponentiation
and root extraction of complex numbers examples
|
| Example: |
Calculate |
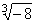 |
using de Moivre's
formula. |
|
|
|
|
|
|
|
| These complex numbers satisfy the equation z3
= -8
and by the Fundamental theorem of algebra, since this equation
is of degree 3, there must be 3 roots. |
| Thus, for
example to check the root zk=2
we cube this solution, |
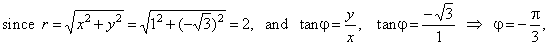 |
| then |
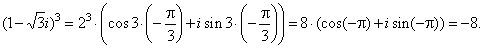 |
|
|
|
| Example: |
Calculate |
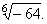 |
|
|
|
|
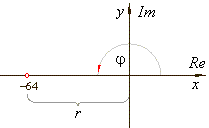
r
= 64 and
j =
p |
 |
|
| |
| |
| thus, |
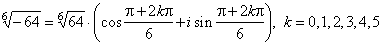 |
| |
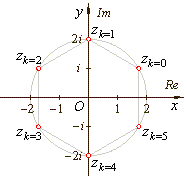
|
 |
|
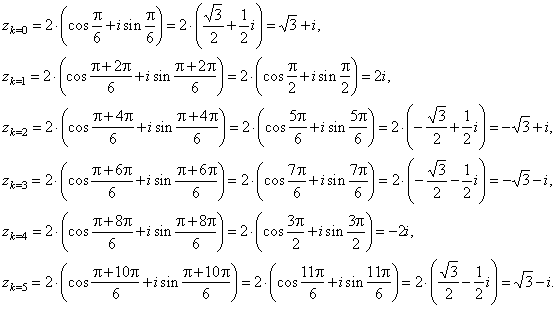 |
| These complex numbers satisfy the equation z6
= -64
and by the Fundamental theorem of algebra, since this equation
is of degree 6, there must be 6 roots. |
|
| Example: |
Calculate |
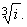 |
|
|
|
|
|
|
|
|
|
| Example: |
Calculate |
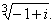 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Functions
contents A
|
|
 |
|
|
|
Copyright © 2004 - 2020, Nabla Ltd.
All rights reserved.
|