|
|
Applications
of differentiation - the graph of a function and its derivatives |
 Extreme
points, local (or relative) maximum and local minimum
Extreme
points, local (or relative) maximum and local minimum |
|
The
first derivative test |
|
The
second derivative test and concavity |
 Finding and classifying
critical (or stationary) points
Finding and classifying
critical (or stationary) points |
|
Finding extreme points |
|
Points
of inflection |
|
Finding points
of inflection |
|
Finding and classifying
critical (or stationary) points, example |
|
|
|
|
|
|
| Extreme
points, local (or relative) maximum and local minimum |
| The
derivative f '(x0)
shows the rate of change of the function with respect to the variable x
at the point x0. |
| The
derivative f '(x)
is equal to the slope of the tangent line at x.
If the derivative is positive, the function is increasing
at that point. If it is negative, the function is decreasing. |
| A
point on the graph of a function at which its first derivative is zero,
so that the tangent line is parallel to the x-axis,
is called the stationary point or critical
point. |
| A
point at which a function attains its maximum value among all points
where it is defined is called a global (or
absolute) maximum. A
point at which a function attains its minimum value among all points
where it is defined
is a global (or absolute) minimum. |
|
| The
first derivative test |
| Let
f (x)
be a function and x
= c
a critical point of f. |
| Test
for local maximum. If in some
neighborhood of c
the derivative f '(x)
is positive to the left of c
and negative
to the right, then c
is a local (or relative) maximum of f. |
| Test
for local minimum. If in some
neighborhood of c
the derivative f '(x)
is negative to the left of c
and positive
to the right, then c
is a local (or relative) minimum of f. |
| In
the figure below, xmax
denotes a local maximum and xmin
a local minimum. The change of f '(x)
from positive
to negative to positive is shown by tangents. |
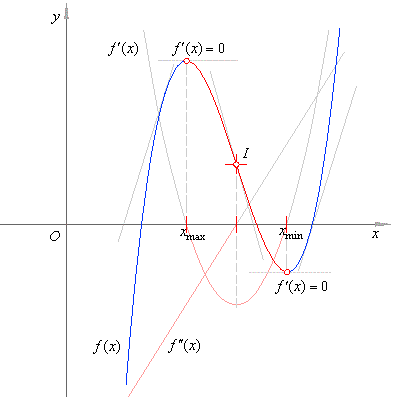 |
| A
stationary (or critical) point at which the first derivative of a
function changes sign, so that its graph does not
cross a tangent parallel to the x-axis,
is called the turning point. |
| If
the second derivative is negative ( f ''(x)
< 0 ) at a stationary point, it is
local maximum of the function, and if
the second derivative is positive ( f ''(x)
> 0 ), it is local minimum, as
shows the above figure. |
|
| The
second derivative test and concavity |
| A
function is said to be concave
down on an interval
if its first derivative is decreasing on the interval. |
| At
the same time the second derivative of the function is negative on the
interval. |
| A
function is said to be concave
up on an interval if
its first derivative is increasing on the interval. |
| At
the same time the second derivative of the function is positive on the
interval. |
| The
second derivative test shows when a critical point c
is a local maximum or local minimum. |
|
(1) If f '(c)
equals 0
and f ''(c)
< 0, then x
= c is a
local maximum. |
|
(2) If f '(c)
equals 0
and f ''(c)
> 0, then x
= c is a
local minimum. |
|
(3) If f '(c)
equals 0
and f ''(c)
= 0, then c
may be a
local maximum,
local minimum or point of inflection. |
| Thus,
the
second derivative is inconclusive when f ''(c)
= 0. |
|
| Finding
and classifying critical or stationary points |
| Therefore,
to
find extreme points of a differentiable function y
= f
(x)
calculate its derivative, equate it to zero and
solve for x. |
| Roots
of the
equation f '(x)
= 0
are potential abscissas of, maximums, minimums and points of
inflections. |
| So,
to classify these points we
plug each root x0,
x1,
x2,
. . . into
successive higher order derivatives, starting with
the
second derivative. |
| If
first of higher order derivatives that do not vanishes (becomes 0)
at this point (say
x0)
is of even order, then the
function
has either maximum or minimum at that point, precisely |
|
- a
local maximum if f (2n)(x0)
< 0
or a local
minimum if f (2n)(x0)
> 0. |
| If
first of the higher order derivatives that do not vanishes at this point is of
odd order, then the function has not
extreme
points (extremal points or extrema) at that point at all. |
|
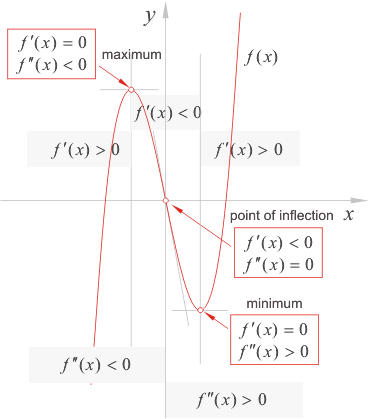
| Points
of inflection |
| A
point of the graph of a function at which it crosses its tangent, and
concavity changes from up to down or vice
versa is called the point of inflection. |
| The
second derivative of the function is zero and changes its sign at the
point of inflection, as can be seen in the
figure above. |
| Therefore,
to
find points of inflection of a differentiable function y
= f
(x)
calculate its second derivative, equate
it
to zero and
solve for x. |
| A
root of the equation
f ''(x) = 0
is the abscissa of a point of inflection if first
of the higher order derivatives that do
not
vanishes at this point is of odd order. |
 |
|
| Finding and classifying
critical or stationary points example |
| Example: Find
extreme points and points of inflection of the quintic y
= -x5 +
5x4 -
7x3 + x2 +
4x
-1
and sketch its graph. |
| Solution: To
rewrite given polynomial from general into translatable form, and this
way determine its source form,
we first calculate the coordinates of translation |
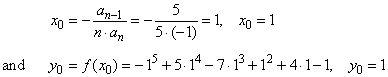 |
| then,
plug x0
and y0
into |
| y
+ y0 = a5(x + x0)5
+ a4(x + x0)4
+ a3(x + x0)3 + a2(x
+ x0)2 + a1(x +
x0) + a0 |
| to get the source form of the given polynomial |
| y
+ 1 = -
1(x + 1)5 + 5(x + 1)4 -
7(x + 1)3 + (x + 1)2 + 4(x + 1)
-
1, |
| what
after expanding and reducing gives y
= -
x5 + 3x3,
the source quintic. |
| Therefore,
we can write
y
= -x5 +
5x4 -
7x3 + x2 +
4x
-1 |
|
or y
-
1
= - (x -
1)5 + 3(x -
1)3 or
f (x)
= - (x -
1)5 + 3(x -
1)3 +
1. |
| To
find the extreme points, calculate the first derivative of the above
expression set it to zero and solve for x, |
| f
' (x) = -
5(x -
1)4 + 9(x -
1)2 = -
(x -
1)2 · [5(x -
1)2 -
9] |
| then
we set
f
' (x) = 0,
-
(x -
1)2 · [5(x -
1)2 -
9] = 0 |
|
what yields, x1
= 1,
x2
= 1 -
3/Ö5
and x3
= 1 + 3/Ö5
as potential abscissas of the extreme points. |
| To
check if x1
= 1
is the abscissa of the extreme point, plug it into
successive higher order derivatives, starting with
the
second derivative. Thus, |
| f
'' (x) = -
20(x -
1)3 + 18(x -
1) = -
2(x -
1) · [10(x -
1)2 -
9]
since f
'' (1) = 0 |
|
we must proceed with the higher order derivatives, |
| f
''' (x) = -
60(x -
1)2 + 18
so that f ''' (1) =
18
is not 0 |
| what
classifies root x1
= 1
as the abscissa of the point of inflection, as
first of higher order derivatives that do not vanishes
at this point is of odd order. |
| While
roots, x2
= 1 -
3/Ö5
and x3
= 1 + 3/Ö5
plugged into the second derivative respectively yield |
| f
'' (1 -
3/Ö5)
> 0,
so x2
= 1 -
3/Ö5
is the abscissa
of the minimum
|
|
and f
'' (1 + 3/Ö5)
< 0,
so x3
= 1 + 3/Ö5
is the abscissa
of the maximum.
|
| To
find points of inflection of the given quintic we set the second
derivative to zero and solve for x, |
| f
'' (x) = -
20(x -
1)3 + 18(x -
1),
-
2(x -
1) · [10(x -
1)2 -
9]
= 0 |
|
what yields, x1
= 1,
x2
= 1 -
3/Ö10
and x3
= 1 + 3/Ö10 as
possible abscissas of the points of inflection. |
| The
root x1
= 1
we've already classified
as the point of inflection. |
| Then
we plug roots, x2
= 1 -
3/Ö10
and x3
= 1 + 3/Ö10
into the third derivative respectively |
| f
''' (x) = -
60(x -
1)2 + 18,
so
f ''' (1 -
3/Ö10)
¹
0
and
f ''' ( 1 + 3/Ö10)
is not 0 |
| what
classifies roots, x2
and x3
as the abscissas of the points of
inflection. |
| By
plugging the abscissas x1,
x2 and x3
into the given quintic we get the ordinates of the points of inflection. |
| The
graph of the given quintic polynomial and its source function is shown
in the figure below. |
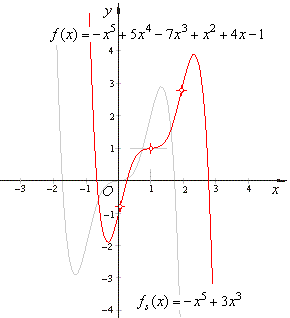 |
|
|
|
|