|
|
Applications
of differentiation - the graph of a function and its derivatives |
Maclaurin's
formula or Maclaurin's theorem |
|
The approximation of the
exponential function by polynomial using Taylor's or Maclaurin's formula |
|
Properties
of the power series expansion of the exponential function |
|
|
|
|
|
|
|
| Maclaurin's
formula or Maclaurin's
theorem |
| The
formula obtained from Taylor's
formula by setting x0
= 0
|
 |
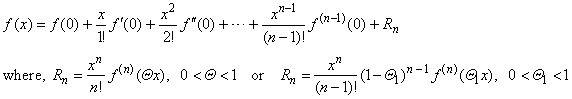| that
holds in an open neighborhood of the origin, is called Maclaurin's
formula or Maclaurin's
theorem. |
|
| Consider
the polynomial
fn(x)
= anxn
+ an -
1xn -
-
-
1 + · · · + a3x3
+ a2x2 + a1x
+ a0, |
| let
evaluate the polynomial and its successive derivatives at the origin, |
| f
(0) =
a0, f '(0) = 1· a1,
f ''(0) = 1· 2a2,
f '''(0) = 1· 2· 3a3, . . .
, f (n)(0) =
n!an |
| we
get the coefficients, |
 |
|
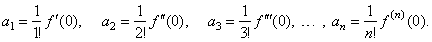| Therefore,
the Taylor polynomial of a function f
centered at x0
is the polynomial of degree n
which has the same
derivatives as f
at x0,
up to order n. |
| If
a
function f
is infinitely differentiable on an interval about a point x0
or the origin, as are for example ex and
sin
x,
then |
|
P0 (x)
= f (x0), |
|
P1 (x) =
f (x0)
+ (x
-
x0)
f ' (x0), |
|
|
| P0,
P1,
P2,
. . . is a sequence of increasingly approximating polynomials for f. |
|
| The
approximation of the exponential function by polynomial using Taylor's
or Maclaurin's formula |
| Example: Let
approximate the exponential function f
(x)
= ex by
polynomial applying
Taylor's
or Maclaurin's
formula. |
| Solution: The
exponential function is the infinitely differentiable function defined
for all real numbers whose |
| derivatives
of all orders are equal ex
so that, f (0)
= 1, f (n)(0)
= 1 and |
 |
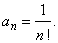Where
Lagrange form |
|
| of the
remainder |
 |
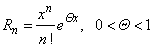so,
using Maclaurin's formula with Lagrange
remainder we get |
|
 |
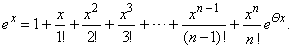| Since
for every real x, |
 |
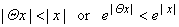then |
|
 |
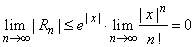| therefore,
the function ex
can be represented by the power series |
 |
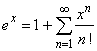| that
is absolutely convergent for all real x. |
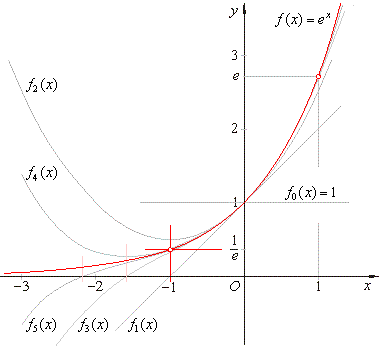
| The approximation of the exponential function by a sequence of polynomials is shown in the figure below. |
 |
|
| Properties
of the power series expansion of the exponential function |
| Since
every polynomial function in the above sequence, f1
(x),
f2 (x),
f3(x),
. . . , fn
(x),
represents translation of its
original or source function, we calculate the coordinates of
translations, x0 and
y0,
to get their source forms. |
| Let's
apply the method and formulas that are revealed and
explored under the 'Polynomial' sections. |
|
Thus, the coordinates of translations are, |
 |
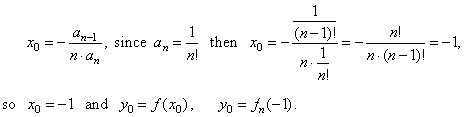| Note
that the above result proves the main property of the polynomial stating
that, an nth
degree polynomial
function and all its successive derivatives to (n
-
1)th order, have constant horizontal translation
x0. |
| Below
listed sequence of the polynomials and corresponding vertical
translations y0
shows that their graphs
approach closer and closer to the point (x0,
y0) or (-1,
1/e) as n
tends to infinity. |
 |
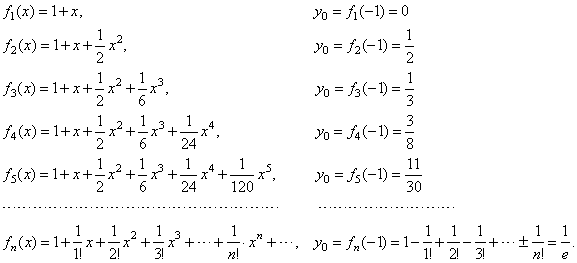| By
plugging the coordinates of translations with changed signs into the
polynomial expressed in the general |
| form
y + y0
= an(x + x0)n
+ an -
1(x + x0)n -
1 + · · · + a2(x +
x0)2 + a1(x + x0)
+ a0, |
| after
expanding and reducing the expression, we get the source polynomial
function passing through the |
| origin.
The above expression we can write as |
| fs(n)(x)
+ y0 = fn(x + x0)
or fs(n)(x)
= fn(x + x0) -
fn(x0), |
| For
example, we obtain the source quadratic fs2(x)
from the expression |
| fs2(x)
+ y0 = f2(x + x0)
or fs2(x)
= f2(x + x0) -
y0 that is, |
 |
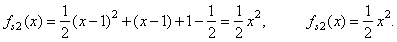| The
same way we get the source function of every polynomial as listed below. |
 |
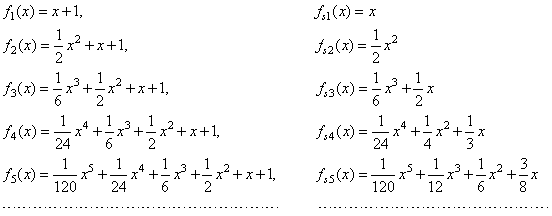| To
prove that expressions on the left and the right side of the same row
represent the same curve plug x0 and
y0
into the source polynomial to get its translated form or, we can check
if the derivative
at x0
= - 1
of the
left side polynomial
is
equal to the derivative at x
= 0 of the source polynomial
(the graph of which passes
through the origin) on the right side. Thus,
for example |
 |
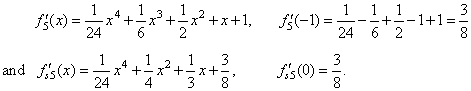| Note
that all polynomials from f1
to fn
in the above sequence have the same horizontal translation x0
= - 1.
|
| Recall
that an nth
degree polynomial function and all its successive derivatives to (n
-
1)th order, have constant horizontal translation
x0. |
| Since
every polynomial in the above sequence represents the derivative of its
successor, that is, |
| f
'n(x)
= fn -
1(x) and thus
f
'n(x0)
= fn -
1(x0). |
| Therefore
as consequence, each x-intercept
of odd polynomial in the sequence determines the abscissa of the
only extreme (minimum) of succeeding even polynomial and the abscissa of
the only point of inflection of succeeding
odd polynomial, as shows the picture above. |
| In
the same way, for example the coefficients, a1,
a2,
and a3
of the source polynomial fs5(x)
are |
 |
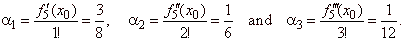| Hence,
the vertical translations y0
of the successive derivatives are, |
|
f4(x0)
= 1! f5´(x0)
= 3/8, f3(x0)
= 2! f5´´(x0)
= 1/3 and
f2(x0)
= 3! f5´´´(x0)
= 1/2 , |
| as
is shown above. |
|
|
|
|
|
