|
|
Higher order derivatives and higher order differentials |
Higher derivatives of composite functions |
|
Higher derivatives of composite functions examples |
|
Higher derivatives of implicit functions |
|
Higher derivatives of implicit functions examples |
|
|
|
|
|
|
|
|
Higher derivatives of composite functions |
| If
y = f (u) and
u
= g (x) such that
f
is differentiable at u
and g
is differentiable at x
then,
we differentiate the composite
function y
[u (x)] by
applying the chain rule |
| y'
(x)
= y' (u) · u' (x). |
| To
get the second derivative of the given composite function we differentiate
the above expression using both the
product rule and the chain rule |
| y''
(x)
= y' (u) u'' (x) +
u'
(x) [y'' (u) u' (x)]
= y'' (u)
[u' (x)] 2 +
y' (u) u'' (x). |
| Proceeding
the same way we get the third derivative of the composite function |
| y'''
(x)
= y''' (u)
[u' (x)] 3
+
3y'' (u) u' (x) u'' (x) +
y' (u) u''' (x) and so on. |
|
|
Higher derivatives of composite functions
examples |
| Example:
Find
the second derivative of |
 |
|
|
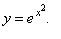Solution: |
 |
|
|
|
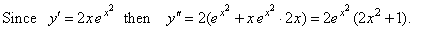Example:
Find
the second derivative of y
=
sin2x.
|
|
Solution: |
y'
= 2sin x cos x,
y''
= 2[sin x( -sin
x)
+ cos
x cos x]
= 2(cos2x
-
sin2x)
= 2cos 2x. |
|
|
|
Higher derivatives of implicit functions |
| The
first derivative of a function y = f(x)
written implicitly as F(x,
y) = 0
is |
 |
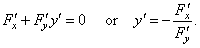| In
words,
differentiate the implicit equation with respect to both variables at the
same time such that, when differentiating
with respect to x,
consider
y
constant, while
when differentiating with respect to y,
consider x constant
and multiply by y'. |
| We
use this method to differentiate the
above equation to extract the second derivative |
 |
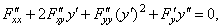| and
after substituting
the value for y' |
 |
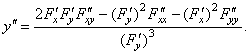| Differentiating
the second
derivative equation above, applying the same method, we can get
the third derivative of
an implicit function and so on. |
|
|
Higher derivatives of
implicit
functions examples |
|
Example:
Find
the second derivative of y2
=
2px
or written implicitly
y2
-
2px
=
0
as
F(x,
y) = 0.
|
|
Solution: |
The
first derivative,
2yy'
= 2p
or
yy'
= p,
y'
= p/y. |
|
|
The second derivative,
(y' )2
+ yy''
= 0 => y''
= -
(y' )2
/ y |
|
and
by substituting y'
= p/y,
y''
= -
p2
/ y3.
|
| We
can obtain the same result using the above formulas.
Therefore,
first calculate
|
 |
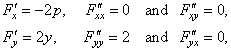| and
plug these values into the formulas for the first and the second
derivative |
 |
|
|
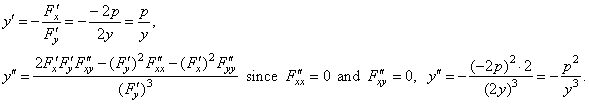Example:
Find
the second derivative of y
-
tan-1y
=
x.
|
|
Solution:
|
 |
|
|
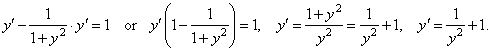The second derivative, |
 |
|
|
|
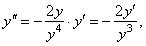| Again,
we
can obtain the same result using the above formulas.
|
|
|
