|
|
The chain rule
applications |
 Logarithmic differentiation
Logarithmic differentiation |
|
Logarithmic differentiation examples |
 Derivative of a composite exponential function
Derivative of a composite exponential function |
|
Use of the logarithmic differentiation |
|
Derivatives of composite functions examples |
|
|
|
|
|
|
|
| Logarithmic differentiation |
|
The derivative of the logarithm of
a function y
= f (x)
is called the logarithmic derivative of the
function, thus
|
|
|
| Therefore, the logarithmic derivative
is the derivative of the logarithm of a given function. |
|
|
Logarithmic differentiation examples |
|
Example:
Find
the derivative of the function f
(x)
= ln (sin x).
|
| Solution: |
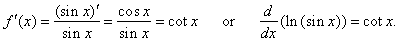 |
|
|
|
Example:
Find
the derivative of the function f
(x)
= ln (cos x).
|
| Solution: |
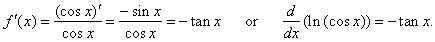 |
|
|
| Example:
Find
the
logarithmic derivative
of the function |
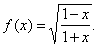 |
|
|
| Solution:
Since the
logarithm of the given function |
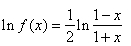 |
|
| then
differentiating both the left and the right side of the above
expression, obtained is |
|
|
|
| Derivative
of a composite exponential function |
| We
use the logarithmic differentiation to find derivative of a composite
exponential function of the form, |
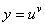 |
| where
u
and v
are functions of the variable x
and u
> 0. |
| By
taking logarithms of both sides of the given exponential expression we
obtain, |
| ln
y
= v
ln
u. |
| Differentiating both sides of the above
equation
with respect to
x |
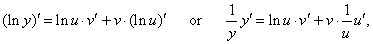 |
|
|
|
|
Use of the logarithmic differentiation |
|
Derivatives of composite functions examples |
| Example:
Find
the
derivative
of the function |
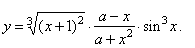 |
|
|
| Solution: |
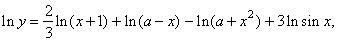 |
|
| by
differentiating both sides of the above equation we get
|
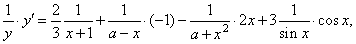 |
| or |
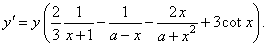 |
|
|
| Example:
Find
the
derivative
of the function |
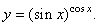 |
|
|
| Solution: |
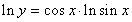 |
|
| by
differentiating both sides of the above equation we get
|
 |
|
| Example:
Find
the
derivative
of the function |
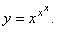 |
|
|
| Solution: |
 |
|
| by
differentiating both sides of the right equation above, we get |
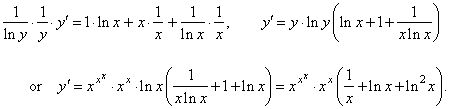 |
|
| Example:
Find
the
derivative
of the function |
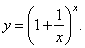 |
|
|
| Solution: |
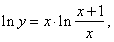 |
|
| by
differentiating both sides of the above equation we get
|
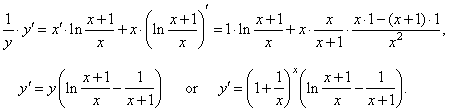 |
|