|
| Differential
calculus |
|
|
|
 Properties
of continuous functions
Properties
of continuous functions |
|
Continuous function definition |
|
Intermediate value theorem - Bolzano's theorem |
|
Existence of roots |
|
Extreme value theorem |
|
Monotone function |
|
|
|
|
|
|
| Properties
of continuous functions |
| Continuous
function definition |
| A
real function
y = f (x)
is continuous at a point a
if it is defined at x =
a
and |
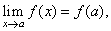 |
| that
is, if for every e
> 0 there is a d(e)
> 0 such that |
f
(x)
-
f
(a)
| < e
whenever | x
-
a | < d(e). |
| Therefore,
if a function changes gradually as independent variable changes,
so that at every value a,
of the independent
variable, the difference between f
(x)
and f
(a)
approaches zero as x
approaches a. |
| Thus,
a function is continuous at a point if both one-sided limits (the
left-handed and right-handed limits) are equal, |
|
|
| that
is, if it is continuous both on the left and on the right at that point. |
| A
point at which the function value is not equal to its limit, as x
approaches that point, is called point
of discontinuity.
A
function having points of discontinuity is discontinuous. |
| A
function is said to be continuous if it is continuous at all
points |
|
| 1.
Intermediate value theorem - Bolzano's theorem |
| If
a function is continuous on the closed interval [a,
b] then it takes every value
between f (a)
and f (b)
for at least
one argument between a
and b. |
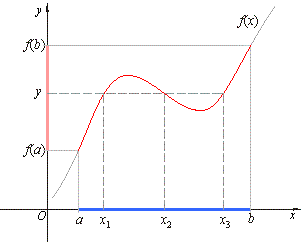
| That
is, for every y
between f
(a)
and f (b)
there exists at least
one argument x
between a
and b whose
function's
value f (x)
= y, as
shows the figure below. |
|
|
|
| 2.
Existence of roots |
| If
a function is continuous on the closed interval [a,
b] then, if f
(a)
and f (b)
have opposite signs, or |
| f
(a)
·
f (b)
< 0, then there exists x
Î
[a, b] such that f
(x) = 0. |
|
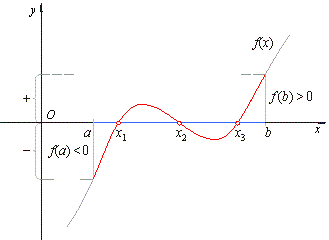
That
is, the function has at least one real root. For example,
inside the closed interval [a, b],
the function shown
in the figure below, has three roots, x1,
x2
and x3,
|
|
that is, f
(x1) = 0, f
(x2) = 0
and f
(x3) = 0 since
f(a)
·
f(b) < 0. |
 |
|
| 3.
Extreme value theorem |
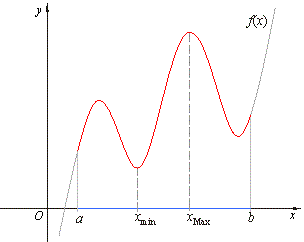
| If
a function is continuous on the closed interval [a,
b] then, there
exist xmin
and xMax
Î
[a, b] such that |
|
for all x
Î
[a, b], values of the function
f
(xmin)
< f
(x) < f
(xMax). |
|
|
| 4.
Monotone function |
|
A continuous
function is monotone on an interval if it is consistently
increasing or decreasing in value,
|
|
so that
either
f
(x1) < f
(x2)
for
all
x1 < x2,
|
|
or
f
(x1) > f
(x2)
for
all
x1 < x2.
|
|
These
may be called strictly monotone
functions to distinguish them from those satisfying either
|
|
f
(x1) < f
(x2)
for
all
x1 < x2,
|
|
or
f
(x1) > f
(x2)
for
all
x1 < x2,
|
| that
are called weakly monotone. |
|