|
| Conic
Sections |
|
|
|
Conics, a Family of Similarly Shaped Curves
- Properties of Conics
|
 Dandelin's
Spheres - proof of conic sections focal properties
Dandelin's
Spheres - proof of conic sections focal properties
|
|
Proof that conic section curve is the hyperbola
|
|
Proof that conic section curve is the parabola
|
|
|
|
|
|
|
| Dandelin Spheres - proof of conic sections focal properties |
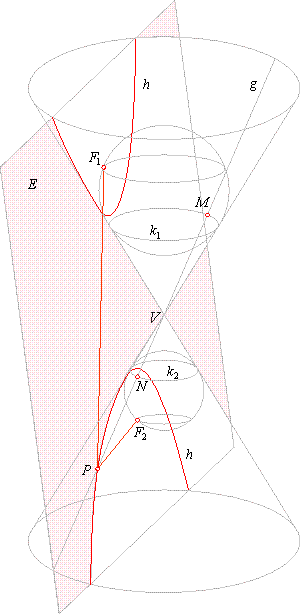
| Proof that conic section curve is the hyperbola
|
| When the intersecting plane is inclined to the vertical
axis at a smaller angle than does the generator of the
|
|
cone, the plane cuts both cones creating the
hyperbola
h which therefore consists of two disjoining
branches
as shows the
right figure.
|
|
Inscribed spheres touch the plane on the same side
at points
F1
and F2
and the cone surface at circles
k1and k2.
|
|
The generator
g
intersects the circles k1and k2, at
points, M and
N, and the intersection curve at the
point
P.
|
By rotating the generator
g
around the vertex V
by
360°,
the point P
will move around and trace both
branches of the hyperbola.
|
|
While rotating, the generator
will coincide with the plane two times and then will have common points
with the curve only at infinity.
|
|
As the line
segments, PF1and
PM are the tangents
segments drawn from P
to the upper sphere, and the segments PF2
and
PN
are the tangents segments drawn to the lower sphere, then
|
|
PM =
PF1
and PN =
PF2.
|
|
Since the planes of
circles k1
and k2, are parallel,
then are all generating segments from
k1to
k2
of equal
length,
so
|
|
MN =
PM -
PN
or PF1
-
PF2
is constant.
|
Thus, the intersection curve is the locus of points in
the plane for which difference of distances from the
two fixed
points F1
and F2, is constant, i.e., the curve is
the hyperbola.
|
|
 |
|
|
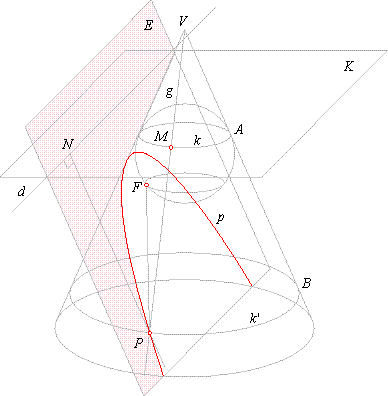
| Proof that conic section curve is the parabola
|
| When the cutting plane is parallel to any generator of one of the cones then we can insert only one sphere into
the cone which will touch the plane at the point F
and the cone surface at the circle
k.
|
|
Arbitrary chosen generating line
g
intersects the circle k
at a point
M,
and the intersection curve p
at a point
P.
The point P lies on the circle
k' which is
parallel with the plane K as shows
the down figure.
|
| By rotating the generator
g
around the vertex
V, the
point P
will move along the intersection curve.
|
|
While the generator approaches
position to be parallel to the
plane
E,
the point
P will move far away from
F.
That shows the basic property of the
parabola that the line
at infinity is a tangent.
|
|
The segments,
PF
and PM
belong to tangents drawn from P
to the sphere
|
|
so, PM
= PF.
|
|
Since planes of the circles,
k
and k'
are parallel to each other and
perpendicular to the section through
the cone
axis, and as the plane E
is parallel to the slanting edge
VB, then
the intersection
d, of planes
E
and
K,
is also
perpendicular to the section
through the cone axis.
|
|
Thus, the perpendicular
PN from
P to the line
d,
|
|
PN =
BA =
PM
or PF =
PN.
|
|
 |
|
|
Therefore, for any point
P
on the intersection curve the distance from the fixed point
F
is the same as it is from the fixed line
d, it proves that the intersection curve is the parabola.
|