|
| Conic
Sections |
|
|
|
Parabola
and Line
|
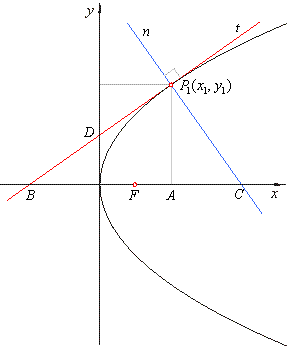
The equation of the tangent and the normal at the point on the parabola |
|
Properties of the parabola
|
|
Polar of the parabola
|
| |
|
|
|
|
|
| The equation of the tangent and the normal at the point on the parabola
|
| In the equation of the line
y
-
y1
= m(
x
-
x1)
through the given point we express the slope m
by the given
|
| ordinate of the tangency point,
|
 |
|
|
|
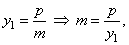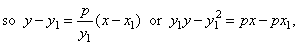
and since the coordinate of the tangency point must
satisfy the equation of the parabola, then
|
|
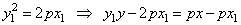
| obtained
is |
y1y
= p(x
+ x1) |
the
equation of
|
|
|
the tangent at the point
P(x1, y1)
on the parabola.
|
| Since
|
 |
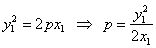the above equation
|
|
|
can be written
using coordinates of the tangency point
|
|
|
|
 |
|
|
As the slope of the normal |
 |
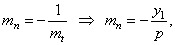then
the equation of the normal at P(x1, y1),
|
|
| |
 |
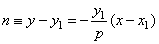or |
 |
|
|
|
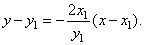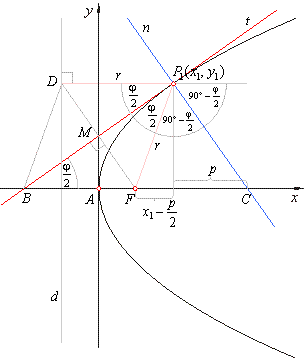
| Properties of the parabola
|
|
Using equations of the tangent and normal expressed by coordinates of
the tangency points and the figure above;
|
|
a) y-intercept
ct
of the tangent equals half of the ordinates of the tangency point, ct
= y1/2. |
b)
the projection
AB
of the segment BP1
of the tangent to the x-axis,
i.e., to the axis of the parabola, is
equal to twice the abscissa
of the tangency point, so |
|
AB
= St
= 2x1 -
the line segment
AB
is called the subtangent. |
|
c) the projection
AC
of the segment CP1
of the normal to the x-axis is equal to the parameter
p, i.e., |
|
AC
= Sn
= p -
the line segment
AC
is called the subnormal. |
As points B
and C
are x-intercepts
of the tangent and the normal their abscissas we determine by solving
corresponding equations for y =
0, so |
| put y =
0 into equation of the tangent, |
 |
|
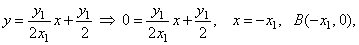| put
y =
0 into equation of the normal, |
 |
|
|
|
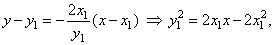| Thus, the focus
F(p/2,
0) bisects the line segment
BC
whose endpoints are x-intercepts of the tangent and
the normal, as shows the figure above. |
|
|
The tangent at
any point on the parabola bisects the angle
j
between focal distance and the perpendicular to the directrix and is
equally inclined to the focal distance and the axis of the parabola. |
|
The
normal at the tangency point bisect the supplementary
angle of the angle
j.
|
|
Since,
DP1
= FP1
= r
= x1
+ p/2,
|
|
and
BF
= FC
= x1
+ p/2
= r, and DP1
|| BC
|
|
then,
following triangles are congruent,
|
|
DBFD
@
DFCP1
@
DFP1D
|
so, the quadrangle
BFP1D
is the rhombus and its
diagonal BP1
bisects the angle j.
|
|
This
property is known as the reflective property of the parabola.
|
|
A light
rays coming in parallel to the axis of a parabolic mirror
(telescope), are reflected so that they all pass through
the focus. Similarly, rays originating at the focus
(headlight) will be reflected parallel to the axis.
|
|
 |
|
|
|
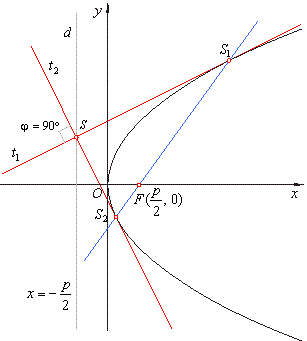
Tangents drawn
at the endpoints of a focal chord intersect at right angles on the
directrix. |
|
a)
Solving the system of equations of tangents,
|
|
|
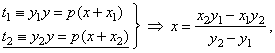
x
is the abscissa of the intersection S
of tangents.
|
|
The slope of
the focal chord line through tangency points,
|
|
|
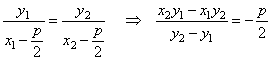
therefore,
x = -
p/2 is the abscissa
of the intersection S(-
p/2, y) and the
equation of the directrix
d.
|
|
b)
The tangent to the parabola which passes through
intersection
S, which
lies on the directrix, must satisfy tangency condition,.e.,
|
|
 |
|
 |
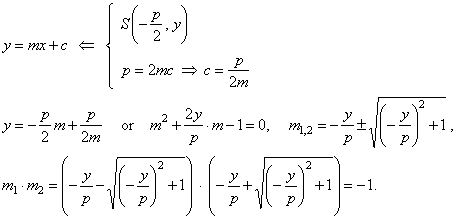| Thus,
satisfied is condition for perpendicularity, m1
· m2
=
-
1 => j
=
90°. |
|
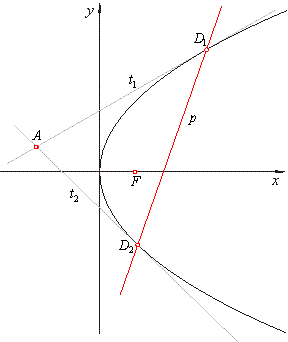
| Polar of the parabola
|
|
The polar p
of a point A(x0, y0), exterior to the parabola
y2 = 2px, is the secant through the contact
points of the
tangents drawn from the point A
to the parabola. |
|
The tangency points
D1(x1, y1)
and D2(x2, y2)
and the point A
satisfy the equations of tangents,
|
|
t1
:: y1y0
= p(x0
+ x1)
and t2
::
y2y0
= p(x0
+ x2).
|
|
Subtracting
t2
-
t1,
|
|
y0(y2
-
y1)
= p[(x0
+ x2)
- (x0
+ x1)]
|
|
|
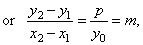
obtained is the slope of the polar. By plugging the slope into equation of the line through the given point
|
 |
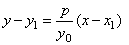or
y0y
= y1y0
+ px -
px1 |
|
|
since y1y0
= p(x0
+ x1),
|
| then
|
y0y
= p(x
+ x0) |
the
equation of the
polar.
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
| Conic
sections contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
