|
| Conic
Sections |
|
|
|
Parabola
|
Transformation of the equation of a parabola
|
|
Equation of a translated parabola - the standard form
|
|
Parametric equations of the parabola
|
|
Equations of the parabola examples |
|
|
|
|
|
|
| Transformation of the equation of a parabola
|
| The equation
y2 = 2px,
p < 0
represents the parabola opens to the left since must be y2
> 0. Its axis of
symmetry is the x-axis. |
| If variables
x and
y change the role obtained is the parabola whose axis of
symmetry is y-axis.
|
| For
p >
0
the parabola opens up, if
p <
0
the parabola opens down as shows
the below figure. |
 |
|
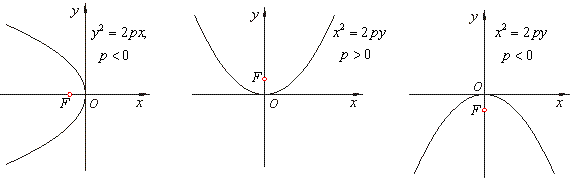This parabola we often write
y = ax2,
where
a = 1/(2p) , with the focus at
F(0,
1/(4a)) and the directrix |
| y =
-1/(4a).
This parabola is a function since a vertical line crosses its graph at only one point.
|
|
| Equation of a translated parabola - the standard form
|
| By parallel shifting of the parabola
y2 = 2px in the direction of the coordinate axes the vertex of the parabola
can be brought at a point A(x0, y0) while coordinates
x
and y of every point of the parabola changes by the |
|
value of the
translations x0 and
y0, so that equation of the translated
parabola is
|
|
|
|
If p >
0
the parabola
opens to the right and if p
< 0
the
parabola opens to the left.
|
|
If the focal parameter
p = 2a
then the above equation
|
|
becomes,
(y
-
y0)2 =
4a(x
-
x0).
|
|
The translated parabola with the axis parallel to the
x-axis
can also be written as
|
|
x =
ay2
+ by
+ c.
|
|
 |
|
|
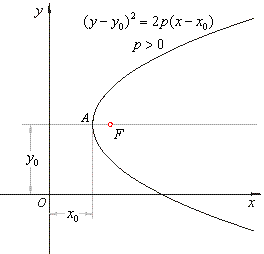| Equations of the parabola written in the general form |
| a) the axis of the parabola parallel to the
x-axis
|
|
b) the axis of the parabola parallel to the
y-axis |
|
Ay2
+ Bx + Cy +
D =
0, A and
B not
0, |
|
Ax2
+ Bx + Cy +
D =
0, A and
C not 0 |
|
or x =
ay2
+ by
+ c,
a not 0. |
|
or
y =
ax2
+ bx
+ c,
a not 0. |
|
| Note
that the parabola has equation that contains only one squared term. |
|
| Parametric equations of the parabola
|
| Parametric equations of the parabola
y2 =
4ax
with the vertex A
at the origin and the focus F(a,
0), and of its translation (y
-
y0)2 =
4a(x
-
x0)
with the vertex A(x0, y0)
and the focus F(x0
+ a, y0)
written |
| respectively
are, |
 |
|
 |
|
|
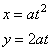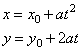| Parametric equations of the parabola
x2 =
4ay
with the vertex A
at the origin and the focus F(0,
a), and of its translation
(x
-
x0)2 =
4a(y
-
y0)
with the vertex A(x0, y0)
and the focus F(y0,
y0
+ a) written |
| respectively
are, |
 |
|
 |
|
|
|
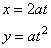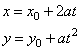| Equations
of the parabola examples |
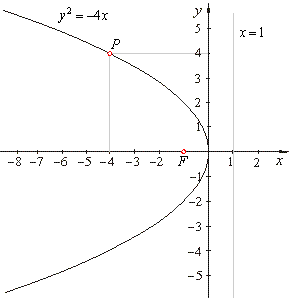
| Example:
Write equation of the parabola
y2 = 2px
passing through the point P(-4,
4) and find the focus,
the equation of the directrix and draw its graph. |
|
|
|
Solution:
The coordinates of the point P
must satisfy the equation of the parabola
|
|
P(-4,
4)
=>
y2 =
2px
|
|
42 = 2p(-4)
=> p =
-2
|
|
thus, the
equation of the parabola y2 =
-4x.
|
|
The coordinate
of the focus,
|
|
since F(p/2,
0) then
F(-1,
0).
|
|
The equation of the directrix,
as x =
- p/2,
x =
1.
|
|
 |
|
|
| Example:
Into a parabola y2 =
2px
inscribed is an equilateral triangle whose one vertex coincides with the
vertex of the parabola and whose area A =
243Ö3.
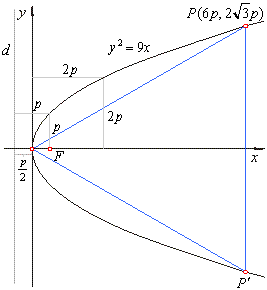
Determine equation of the parabola and remaining vertices of the triangle. |
Solution:
Let write coordinates of a point
P
of the
parabola as elements of the equilateral triangle
|
|
|
As the point P
lies on the parabola then
|
|
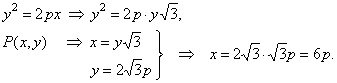
The area of the equilateral triangle we express by
coordinates of
P
|
|
|
 |
|
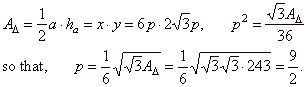
| Show
the parameter of the parabola by the side of the triangle, |
 |
|
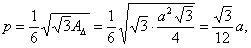| and
the vertices of the triangle P(6p,
2Ö3p) and
P'(6p,
-2Ö3p)
so that, P(27,
9Ö3) and
P'(27,
-9Ö3). |
| Therefore,
the equation of the parabola y2 =
2px or
y2 = 9x. |
|
|
|
|
|
|
|
|
|
|
| Conic
sections contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
