|
| Conic
Sections |
|
|
|
Hyperbola
and Line
|
 Properties of the hyperbola
Properties of the hyperbola
|
|
The area of a triangle which the tangent at a point on the hyperbola forms with
asymptotes |
|
The tangency point bisects the line
segment of the tangent between
asymptotes |
|
The parallels to the asymptotes through the tangency point intersect asymptotes |
 Hyperbola and
line examples
Hyperbola and
line examples
|
|
|
|
|
|
|
| Properties of the hyperbola
|
| -
The area of a triangle which the tangent at a point on the hyperbola forms with
asymptotes, is of constant
|
|
value A
= a ·
b.
|
|
|
| Since one vertex of the triangle is the origin
O(0, 0) then
the formula for the area, AD=
(x2y1
-
x1y2)/2
or |
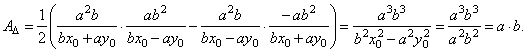 |
|
| -
The tangency point bisects the line
segment AB
of
the tangent between
asymptotes. |
|
The abscissa of the midpoint of the segment
AB,
|
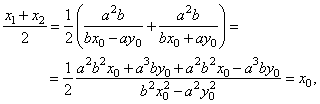
|
| equals the abscissa of the tangency point.
|
|
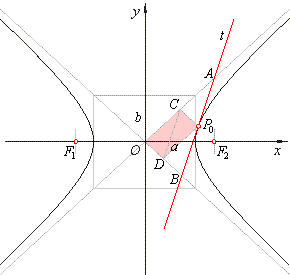
-
The parallels to the asymptotes through the
|
|
tangency point intersect asymptotes at the points,
|
|
C
and
D such
that,
|
|
OC
= AC and
OD
= BD
.
|
|
 |
|
| Therefore, if given are asymptotes and the tangency point
P0, we can construct the tangent by drawing the
parallel to the asymptote
y = (b/a) · x
through P0
to D. Mark endpoint
B
of segment OB
taking D
as the midpoint. Thus, the line segment P0B determines the tangent line. |
| On a similar way we could determine intersection
A,
of the tangent and another asymptote, using point C. |
| Since
triangles, ODC,
DP0C,
DBP0 and
CP0A,
are congruent, it follows that the area of the parallelogram
ODP0C
is equal to half of the area of the triangle
OBA, i.e.,
A
= (a ·
b) / 2. |
|
| Using this property we can derive
the equation of the equilateral or rectangular hyperbola with the
coordinate |
|
axes as its
asymptotes.
|
As the asymptotes of an equilateral hyperbola are
mutually perpendicular then the given parallelogram is
the rectangle.
|
| And since the axes of the equilateral hyperbola are equal
that is a
= b, then
the area A
= a2
/ 2.
|
|
Then, for every point in the new coordinate
system
|
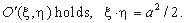
|
|
If we now change the coordinates into
x
and y,
and denote the constant by c, obtained is
|
|
|
|
the equation of
the equilateral or rectangular hyperbola
with the coordinate axes as its
asymptotes.
|
|
 |
|
|
| Hyperbola and line examples
|
| Example:
Determine the semi-axis
a
such that the line
5x
-
4y
-
16 = 0 be the tangent of the hyperbola |
| 9x2
-
a2y2 = 9a2. |
|
Solution:
Rewrite the equation
9x2
-
a2y2 = 9a2 | ¸
9a2
|
|
|
| and the equation of the tangent
5x
-
4y
-
16 = 0
or |
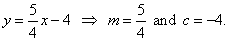 |
|
| Then,
plug the slope and the intercept into tangency condition,
|
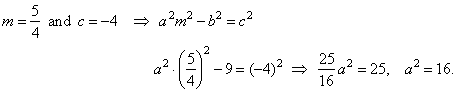 |
| Therefore,
the given line is the tangent of the hyperbola |
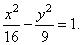 |
|
|
| Example:
The line 13x
-
15y
-
25 = 0 is the tangent of a hyperbola with linear eccentricity (half the focal
distance) cH =
Ö41.
Write the equation of the hyperbola.
|
| Solution:
Rewrite the equation 13x
-
15y
-
25 = 0
or |
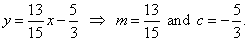 |
|
| Using
the linear eccentricity |
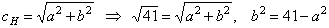 |
|
| and
the tangency condition |
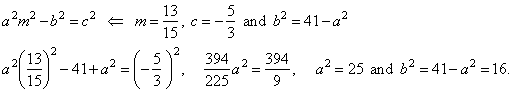 |
| Thus,
the equation of the hyperbola, |
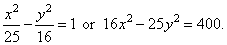 |
|
|
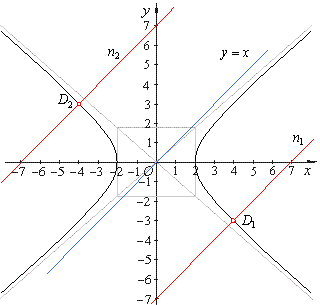
| Example:
Find the normal to the hyperbola
3x2
-
4y2 = 12 which is parallel to the line
-x +
y = 0.
|
|
Solution:
Rewrite the equation of the hyperbola
|
|
3x2
-
4y2 = 12
| ¸12
|
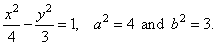
|
|
The slope of the normal is equal to the slope of
the given line,
|
|
y =
x
=>
m
= 1,
mt =
-1/mn,
so mt =
-1
|
|
applying the tangency condition
|
|
a2m2
-
b2 = c2
<= mt =
-1,
a2 =
4 and
b2 = 3
|
|
4·(-1)2
-
3 = c2
=> c1,2 = ±1
|
|
tangents, t1
::
y =
-x
+ 1 and
t2
::
y =
-x
-
1.
|
|
The points of
tangency,
|
|
 |
|
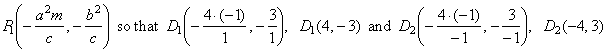
|
| The
equations of the normals, |
| D1(4,
-3)
and m =
1
=>
y -
y1 = m ·(x
-x1),
y +
3 = 1·(x
- 4)
or n1
::
y = x -
7, |
| D2(-4,
3)
and m =
1 =>
y -
y1 = m ·(x
-x1),
y -
3 = 1·(x
+ 4)
or n2
::
y =
x + 7, |
|
|
|
|
|
|
|
|
|
|
| Conic
sections contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |