|
| Conic
Sections |
|
|
|
Ellipse
and Line
|
 Polar and pole of the ellipse
Polar and pole of the ellipse
|
|
Equation of the polar of the given
point
|
 Ellipse and line examples
Ellipse and line examples
|
|
|
|
|
|
|
| Polar and pole of the ellipse
|
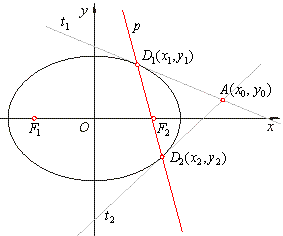
| If from a point A
(x0, y0), exterior to the ellipse, drawn are tangents, then the secant line passing through the
contact points, D1(x1, y1) and
D2(x2, y2) is the polar of the point
A. The point
A is called the
pole of the |
| polar,
as shows the right figure. |
| Coordinates of the point
A(x0, y0) must satisfy the
equations of tangents, thus |
| t1 ::
b2x0x1
+ a2y0y1
= a2b2 |
| t2 ::
b2x0x2
+ a2y0y2
= a2b2 |
|
and after
subtracting
t1
-
t2
|
|
b2x0(x2
-
x1)
+ a2y0(y2
-
y1)
= 0
|
| obtained
is |
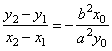 |
|
|
|
 |
|
|
the slope of the secant line through points of contact
D1and
D2.
|
|
Thus, the equation of the secant line
|
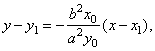
|
and after rearranging |
|
| b2x0x
+ a2y0y
= b2x0x1
+ a2y0y1,
since b2x0x1
+ a2y0y1
= a2b2 |
| follows |
b2x0x
+ a2y0y
= a2b2 |
the
equation of
the polar p
of the
point A(x0, y0). |
|
|
| Ellipse and line examples
|
| Example:
At a point A(-c,
y
> 0) where c
denotes the focal distance,
on the ellipse
16x2
+ 25y2 = 1600
drawn is a tangent to the ellipse, find the area of the triangle that tangent forms by the coordinate axes. |
| Solution:
Rewrite the
equation of the ellipse to the standard form 16x2
+ 25y2 = 1600 | ¸
1600 |
|
|
| We calculate the ordinate of the point
A
by plugging the abscissa into equation of the ellipse
|
| x =
-6
=>
16x2
+ 25y2 = 1600, |
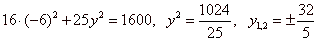
|
|
or, as we know
that the point with the abscise x = -
c
has the ordinate equal to the value of the semi-latus rectum,
|
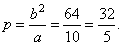
|
|
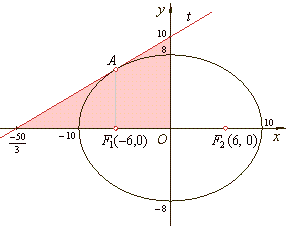 |
|
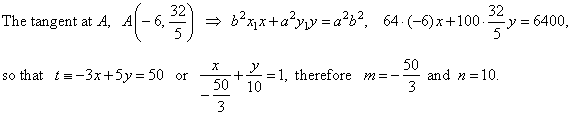 |
| The
area of the triangle formed by the tangent and the coordinate axes, |
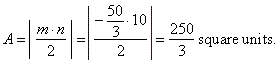 |
|
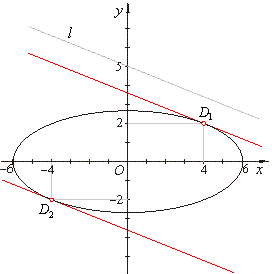
| Example:
Find a point on the ellipse
x2
+ 5y2 = 36 which is the closest, and which is the farthest from the
line 6x + 5y - 25 =
0. |
Solution:
The tangency
points of tangents to the ellipse which are parallel with the given
line are, the
closest and the farthest points from the line.
|
| Rewrite
the equation of the ellipse to determine its axes, |
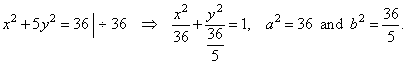 |
| Tangents and given line have the same slope, so |
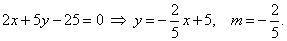 |
| Using the tangency condition, determine the intercepts
c, |
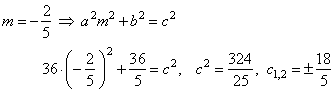 |
|
therefore, the
equations of tangents,
|
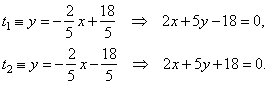
|
|
 |
|
Solutions of the system of equations of tangents to the ellipse determine the points of contact, i.e., the
closest and the farthest point of the ellipse from the given line, thus |
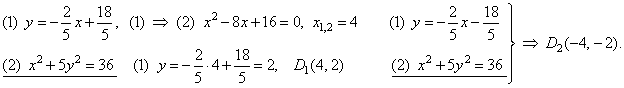 |
|
| Example:
At which points
curves, x2
+ y2 = 8 and
x2
+ 8y2 = 36, intersect? Find the angle between two
curves. |
| Solution:
Given curves are the circle and the
ellipse. The solutions
of the system of their equations determine the intersection points, so |
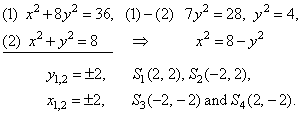 |
|
Angle between two curves is the
angle between tangents drawn
to the curves at their point of
intersection.
|
|
The tangent to the circle at the intersection
S1,
|
|
S1(2,
2) =>
x1x
+ y1y =
r2,
2x +
2y = 8
|
|
or tc
::
y =
-
x
+ 4
therefore, mc
= -1.
|
|
The tangent to the
ellipse at the intersection
S1,
|
|
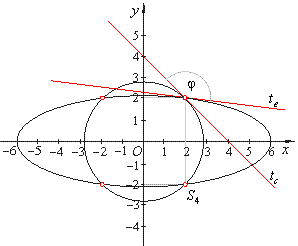 |
|
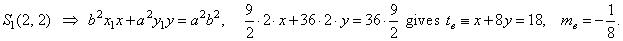 |
| The angle between the circle and the ellipse,
|
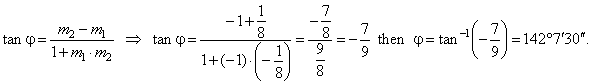 |
|
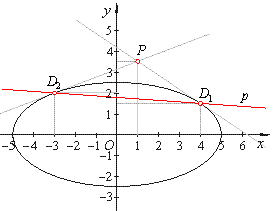
| Example:
The line x
+ 14y
-
25 = 0 is the polar of the ellipse
x2
+ 4y2 = 25. Find coordinates of the pole. |
| Solution:
Intersections of the polar and the ellipse are points
of contact of tangents drawn from the pole P
to ellipse, thus solutions of the system of equations, |
| (1)
x
+ 14y
-
25 = 0 =>
x
= 25 - 14y
=> (2) |
|
(2) x2
+ 4y2 = 25
|
|
|
|
(25 - 14y)2
+ 4y2 = 25
|
|
2y2
-
7y + 6 = 0,
y1 =
3/2 and
y2 =
2
|
|
y1
and y2
=>
x
= 25 - 14y,
x1 =
4 and
x2 =
-3.
|
|
Thus, the points of
contact D1(4,
3/2) and
D2(-3,
2).
|
|
The
equations of the tangents at D1
and
D2,
|
|
 |
|
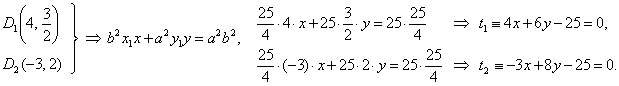 |
|
The solutions of the system of equations t1
and t2
are the coordinates of the
pole P(1, 7/2). |
|
|
|
|
|
|