|
| Conic
Sections |
|
|
|
Ellipse
and Line
|
 Intersection of ellipse and line - tangency condition
Intersection of ellipse and line - tangency condition
|
 Equation of the tangent at a point on the ellipse
Equation of the tangent at a point on the ellipse
|
|
Construction of the tangent at a point on the ellipse
|
 Angle between the focal radii at a point of the ellipse
Angle between the focal radii at a point of the ellipse
|
 Ellipse and line examples
Ellipse and line examples
|
|
|
|
|
|
|
|
| Intersection of ellipse and line - tangency condition
|
| Common points of a line and an ellipse
we find by solving their equations as a system of two equations in two
unknowns, x
and y, |
|
(1) y = mx + c |
|
(2) b2x2 + a2y2
= a2b2 |
| |
|
by plugging (1)
into (2)
=>
b2x2
+ a2(mx + c)2 = a2b2 |
|
after rearranging, (a2m2
+ b2)·x2 + 2a2mc·x
+ a2c2 -
a2b2 = 0 |
| obtained
is the quadratic equation in x.
Thus, the coordinate of intersections are, |
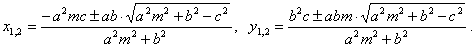 |
|
Using the above solutions follows that a line and an ellipse can have one of three possible mutual positions
depending of the value of the discriminant D
= a2m2
+ b2 -
c2. Thus, if |
|
D > 0, a line and an ellipse
intersect, |
|
D = 0,
or |
a2m2
+ b2 = c2 |
a line is the tangent of the
ellipse and it is tangency
condition. |
|
|
The line touches the ellipse at the tangency point whose coordinates are: |
|
|
|
D < 0, a line and an ellipse
do not intersect. |
|
| Equation of the tangent at a point on the ellipse
|
| In the equation
of the line y
-
y1 = m(x
-
x1)
through a given point P1, the slope m
can be determined using known coordinates (x1,
y1) of the point of tangency, so |
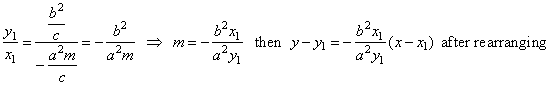 |
| b2x1x
+ a2y1y
= b2x12
+ a2y12,
since b2x12
+ a2y12 =
a2b2
is the condition that P1
lies on the ellipse |
| |
then |
b2x1x
+ a2y1y
= a2b2 |
is the
equation of the tangent at the point P1(x1,
y1)
on the ellipse. |
|
|
| Construction of the tangent at a point on the ellipse
|
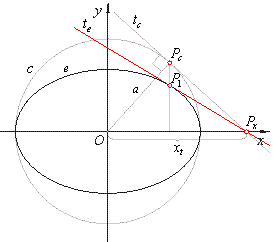
| Draw a circle of a radius
a concentric to the ellipse. Extend the ordinate of the given point to find intersection |
|
with the circle. The tangent of the circle at
Pc
intersects the x-axis at
Px. The tangent to the ellipse at the point
P1on the
ellipse intersects the x-axis at the same point.
|
To prove this, find the
x-intercept of each tangent
analytically. |
Therefore, in both equations of tangents set y = 0 and
solve for x, |
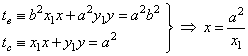 |
|
it is the x-intercept of the tangent
tc
and the tangent te.
|
|
 |
|
|
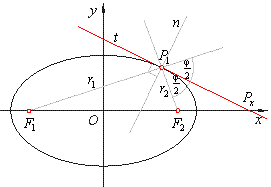
| Angle between the focal radii at a point of the ellipse
|
| Let
prove that the tangent at a point
P1
of the ellipse is perpendicular to the bisector of the angle between the focal radii
r1
and r2.
|
|
Coordinates of points,
F1(-c,
0),
F2(c,
0) and
P1(x1,
y1) plugged
into the equation of the line through two given points determine the lines of the focal radii
|
| r1 =
F1P1
and r2 =
F2P1, |
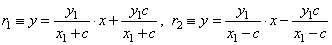 |
|
and the equation of the tangent at the point
P1,
|
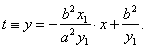
|
|
 |
|
By plugging the slopes of these tree lines into the formula for calculating the angle between lines we find the
exterior angles
j1
and j2
of these lines at P1. |
| Thus, using the condition
b2x12
+ a2y12
= a2b2, that the point lies on the ellipse, obtained is |
 |
| If on the same way we calculate the interior
angle subtended by the focal radii at P1,
and which is the supplementary angle of the angle j, |
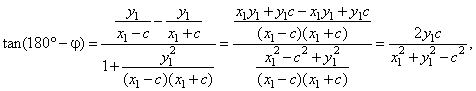 |
| then compare with the
result which will we obtain by using the double-angle formula for the angles
j1
and j2, |
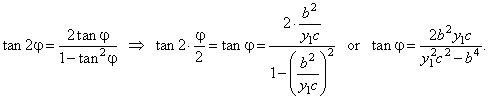 |
| To compare obtained results, we multiply both the
numerator and the denominator of the result for
the supplementary angle by
b2, |
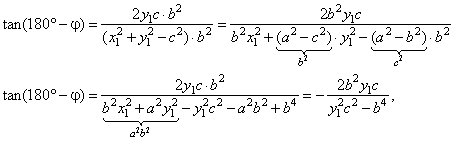 |
| what proved the previous statement. |
| Therefore, the normal at the point
P1
of the ellipse bisects the interior angle between its focal radii. |
|
| Ellipse and line examples
|
| Example:
At a point A(-c,
y
> 0) where c
denotes the focal distance,
on the ellipse
16x2
+ 25y2 = 1600
drawn is a tangent to the ellipse, find the area of the triangle that tangent forms by the coordinate axes. |
| Solution:
Rewrite the
equation of the ellipse to the standard form 16x2
+ 25y2 = 1600 | ¸
1600 |
|
|
| We calculate the ordinate of the point
A
by plugging the abscissa into equation of the ellipse
|
| x =
-6
=>
16x2
+ 25y2 = 1600, |
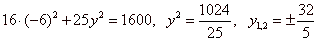
|
|
or, as we know
that the point with the abscise
x = -
c
has the ordinate equal to the value of the
semi-latus rectum,
|
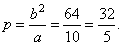
|
|
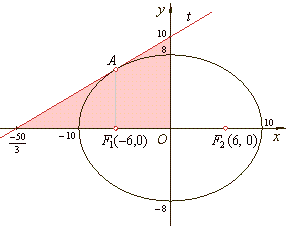 |
|
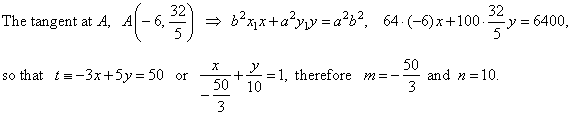 |
| The
area of the triangle formed by the tangent and the coordinate axes, |
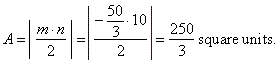 |
|
| Example:
Find a point on the ellipse
x2
+ 5y2 = 36 which is the closest, and which is the farthest from the
line 6x + 5y - 25 =
0. |
Solution:
The tangency
points of tangents to the ellipse which are parallel with the given
line are, the
closest and the farthest points from the line.
|
| Rewrite
the equation of the ellipse to determine its axes, |
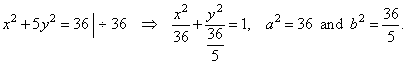 |
| Tangents and given line have the same slope, so |
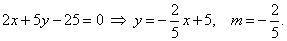 |
| Using the tangency condition, determine the intercepts
c, |
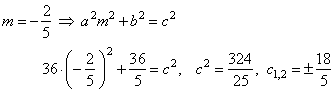 |
|
therefore, the
equations of tangents,
|
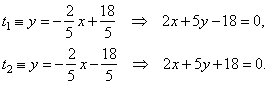
|
|
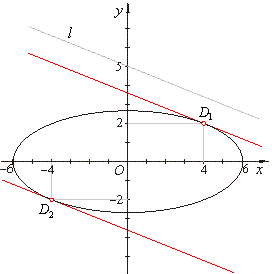 |
|
Solutions of the system of equations of tangents to the ellipse determine the points of contact, i.e., the
closest and the farthest point of the ellipse from the given line, thus |
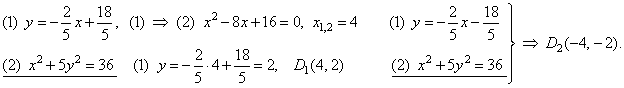 |
|
|
|
|
|
|