|
| Conic
Sections |
|
|
|
Circle
and Line
|
 Mutual position of two circles
Mutual position of two circles
|
 The radical line or the radical
axis
The radical line or the radical
axis
|
 The pole and the polar
The pole and the polar
|
 Angle between two circles
Angle between two circles
|
|
|
|
|
|
|
| Mutual position of two circles
|
Two circles
k1
and k2
intersect if the distance between their centers is less than the sum, but greater than
difference, of their radii. |
| The coordinates of the intersection points of two circles
we calculate by solving their equations as system of two quadratic
equations, |
| k1
::
(x
-
p1)2 + (y -
q1)2 -
r12 = 0
and k2
::
(x
-
p2)2 + (y -
q2)2 -
r22 = 0. |
|
| The radical line or the radical axis |
| Subtracting the second equation
from the first gives equation of the line k1-
k2
= 0 through the intersection |
| points
A and
B of the circles. |
| Coordinates of intersections
A
and B satisfy equations of the circles
k1
and k2 and
the equation of the line k1-
k2
= 0. |
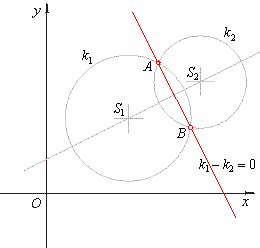
| This line is called the
radical line and represents the
locus or set of all points in the plane of equal power
with respect to two non-concentric circles. |
| The radical line
is a line perpendicular to the line connecting the centers of
the two circles. |
| Since
the slope of the line S1S2, |
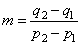 |
|
| then |
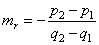 |
is
the slope of the radical line. |
|
|
 |
|
| If two circles touch each other outside then, the radical line
is at the same time their common tangent. |
|
| The pole and the polar
|
| Given is a circle
k
::
x2
+ y2
= r2 and a point
P(x0,
y0) outside the circle. The contact
points of tangents from P
to the circle, are at the same time the intersections of
the given circle k and the circle
k' whose center is the midpoint of the line
segment OP,
that is |
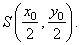 |
| Therefore, the equation of the circle
k'
is
|
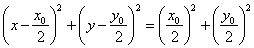 |
|
or, after squaring and reducing
|
| |
k'
:: |
x2
+ y2 - x0
x
- y0
y
= 0. |
|
|
|
Equation of the line through tangency points, which
is perpendicular to the line OP, is
|
| p
::
k
- k'
= 0
or
|
x0
x
+ y0
y
= r2. |
|
|
|
This line is called the
polar
of the
point P
with respect to the circle, and point P
is called the
pole of the polar.
|
|
 |
|
|
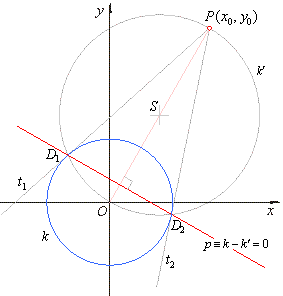
If given is a translated circle
(x
-
p)2 + (y -
q)2 = r2
with the center at the point
S(p,
q), then the equation
of the polar of the point P(x0,
y0) is, |
| |
(x0 -
p) ·
(x -
p) + (y0 -
q) ·
(y -
q) = r2. |
|
|
|
| Angle between two circles
|
Angle between two circles is defined as the angle between the two tangent lines at any of the intersection
points of the circles. |
|
| Example:
Given are circles
k1
::
x2
+ y2 -
4x -
6y
+ 3 = 0 and
k2
::
x2
+ y2 +
6x
+ 4y -
7 = 0,
find their intersections. |
| Solution:
Subtracting given equations of circles gives equation of the line through their intersection points called the radical line or radical axis, |
| k1
::
x2
+ y2 -
4x -
6y
+ 3 = 0 (1) |
| k2
::
x2
+ y2
+ 6x
+ 4y -
7 = 0 (2) |
| |
| k1-
k2
= 0 =>
-10x
-
10y + 10 = 0
or y
= -x +
1. |
| plugging
y
= -x
+ 1 into (1) |
| x2
+ (-x +
1)2 -
4x -
6(-x +
1)
+ 3 = 0 |
|
or 2x2
-
2 = 0,
so x1
=
-1
and
x2 =
1, |
|
y = -x +
1 =>
y1
=
2
and
y2 =
0. |
| thus,
A(-1,
2) and
B(1,
0). |
|
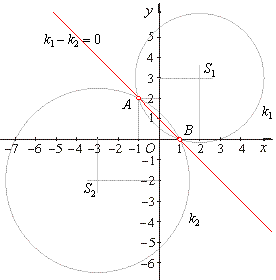 |
|
|
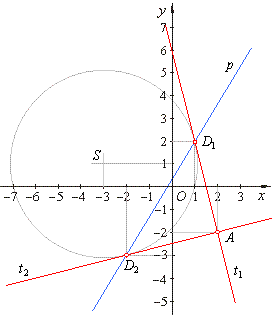
| Example:
From the point
A(2,
-2)
drawn are tangents to the circle
(x +
3)2 + (y -1)2 =
17, find equations of
tangents using the polar and taking the point A
as the pole. |
| Solution:
Coordinates of the point A
plug into equation of the polar, |
| so,
P(x0,
y0)
or
A(2,
-2),
S(-3,
1)
and
r2
= 17 |
| (x0 -
p) ·
(x -
p) + (y0 -
q) ·
(y -
q) = r2 |
| (2 +
3)
·
(x +
3) + (-2 -
1) ·
(y -
1) =
17, |
| which
gives, |
| p
::
5x
-
3y
+ 1
= 0 -
the equation of the polar. |
By solving system of equations of the polar and the circle
we calculate coordinates of points of contact, |
|
(1) 5x
-
3y
+ 1
= 0 |
|
(2) (x +
3)2 + (y -1)2 =
17 |
| |
| it
follows that, D1(1,
2) and
D2(-2,
-3). |
|
 |
|
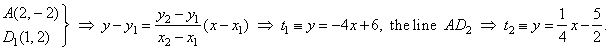 |
|
|
|
|
|
|