|
| Conic
Sections |
|
|
|
Circle
and Line
|
 Line circle intersection
Line circle intersection
|
 Equation of a tangent at a point
of a circle with the center at the origin
Equation of a tangent at a point
of a circle with the center at the origin
|
 Equation of a tangent at a point of a translated circle
Equation of a tangent at a point of a translated circle
|
|
|
|
|
|
|
|
| Circle
and Line
|
| Line circle intersection |
| A
line and a circle in a plane can have one of the three positions in relation
to each other, depending on the distance d
of the center S
(p,
q) of
the circle |
| (x
-
p)2 + (y -
q)2 = r2 from
the line Ax
+ By + C = 0, |
| where the formula for the distance: |
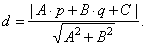 |
| If the distance of the center of a circle from a line is such that: |
|
d
< r,
then the line intersects the circle in two points, |
|
d
= r,
the line touches the circle at only one point, |
|
d
> r,
the line does not intersect the circle, and they have no common points. |
|
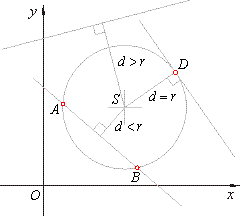 |
|
|
| Example:
At which points the line
x +
5y + 16 = 0
intersects the circle x2
+ y2 -
4x + 2y -
8 = 0. |
| Solution:
To find coordinates of points at which the line intersects the circle solve the system of equations:
|
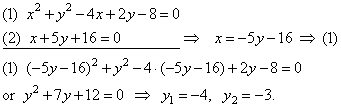 |
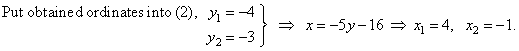 |
| So, the line intersects the circle at points,
A(4, -4)
and B(-1,
-3). |
|
| Example:
Find equation of a circle with the center at
S(1,
20) which touches the
line 8x +
15y -
19 = 0. |
| Solution:
If a line touches a circle then the distance between the tangency point and the center of the circle |
| d
= DS =
r i.e., |
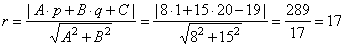 |
| thus,
equation of the circle (x
-
1)2 + (y -
20)2 = 289. |
|
| We can use another method to solve this problem. Since, the
normal n through the center is perpendicular to the tangent
t
then the direction vector sn
is perpendicular to the direction
vector st
.
Therefore, as mt
= sy/sx = -8/15
then |
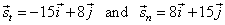 |
|
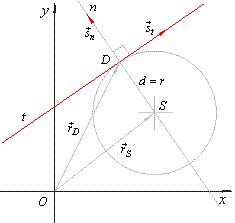 |
|
| so, equation of the normal is |
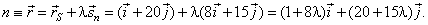 |
As the tangency point
D
is the common point of the tangent and the normal then, putting coordinates of the
radius vector of the normal into equation of the tangent determines a value of the parameter
l
to satisfy that
condition, as |
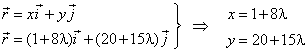 |
| then,
these variable coordinates of the radius vector put into equation of the tangent |
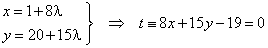 |
| follows
8 ·
(1 + 8l) +
15 · (20 + 15l)
-
19 = 0 => 289l
= 289 => l
= -
1 |
| so, the radius vector of the tangency point |
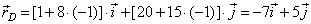 |
|
| therefore
the tangency point D(-7,
5). The radius of the
circle, since |
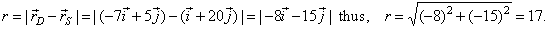 |
| This result we can check
by plugging the coordinates of the tangency point into equation of the circle, that is |
| D(-7,
5) =>
(x
-
1)2 + (y -
20)2 = 289,
(-7
-
1)2 + (5 -
20)2 = 289
=> (-8)2 + (-
15)2 = 289 |
| therefore, the tangency point is the point of the circle. |
|
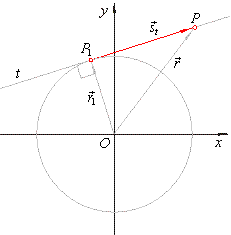
| Equation of a tangent at a point
of a circle with the center at the origin
|
| The direction vector of the tangent at the point P1
of a circle and the radius vector of P1
are perpendicular to each other so their scalar product is zero. |
| Points,
O,
P1
and P
in the right figure, determine vectors, |
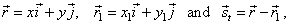 |
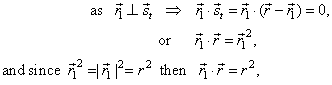 |
|
the
scalar product written in
the components gives,
|
|
x1x
+ y1y = r2
|
| This is
equation of a tangent at the point P1(x1,
y1)
of a circle with the center at the origin. |
|
 |
|
|
| Equation of a tangent at a point
of a translated circle
(x
-
p)2 + (y -
q)2 = r2 |
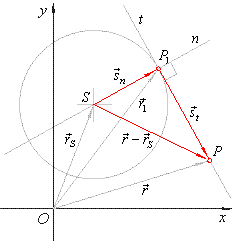
| The direction vector of the tangent at the point P1(x1, y1), of a circle whose center is at the point
S(p,
q), and the direction vector of the normal, are perpendicular, so their scalar product is zero. |
| Points,
O,
S,
P1
and P
in the right figure, determine vectors, |
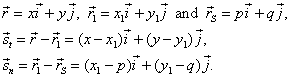 |
| Since |
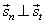 |
their scalar product is zero, that is |
|
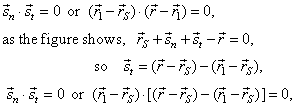 |
|
 |
|
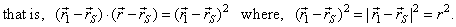 |
| Therefore, |
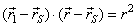 |
is
vector equation of a tangent at the point of a translated
circle, |
|
| or,
when this scalar product is written in the component form, |
(x1
-
p) · (x
-
p) + (y1
-
q)
· (y
-
q) = r2 |
|
| it
represents the equation of the tangent at the point P1
(x1, y1), of a circle whose center is at
S(p,
q). |
|
Example:
Find the angle formed by tangents drawn at points of intersection of a line
x -
y + 2 = 0 and
the circle x2
+ y2 = 10. |
| Solution:
Solution of the system of equations gives coordinates of the intersection points, |
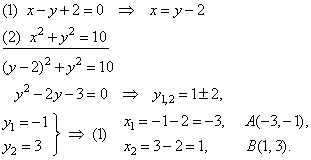 |
| Plug coordinates of
A
and B
into equation of the tangent: |
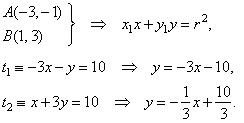 |
|
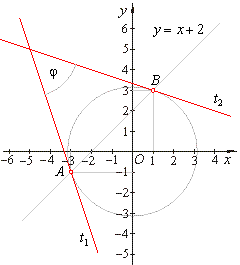 |
|
 |
|
| Example:
At intersections of a line x -
5y + 6 = 0 and the circle
x2
+ y2 -
4x + 2y
-
8 = 0 drown are tangents,
find the area of the triangle formed by the line and the tangents. |
| Solution:
Intersections of the line and the circle are also tangency points. Solutions of the system of
equations are coordinates of the tangency points, |
| (1)
x -
5y + 6 = 0
=>
x = 5y -
6
=> (2) |
| (2)
x2
+ y2 -
4x + 2y
-
8 = 0 |
| |
| (5y
- 6)2
+ y2 -
4(5y - 6) + 2y
-
8 = 0 |
| y2 -
3y + 2 = 0,
=> y1 =
1 and y2
=
2 |
|
x1 = 5 · 1 - 6
= -1,
=> A(-1,
1), |
| x2 =
5 · 2 - 6
=
4, => B(4,
2). |
| Rewrite
the equation of the circle into standard form, |
| (x
-
p)2 + (y -
q)2 = r2 |
|
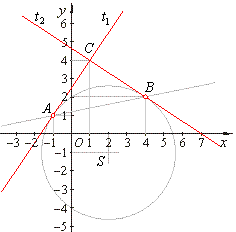 |
|
|
x2
+ y2 -
4x + 2y
-
8 = 0
=> (x
-
2)2 + (y +
1)2 = 13, thus
S(2,
-1) and
r = Ö13. |
| Plug
tangency points A and
B
into equation of the tangent, |
| A( -1,
1) and B(4,
2) => (x1
-
p) · (x
-
p) + (y1
-
q)
· (y
-
q) = r2 |
| (-1
-
2) · (x
- 2) + (1 +
1)
· (y
+
1) =
13
=> t1
:: -
3x + 2y -
5 = 0, |
| (4
-
2) · (x
- 2) + (2 +
1)
· (y
+
1) =
13
=> t2
:: 2x +
3y -
14 = 0. |
| Solution of the system of equations of tangents determines the third vertex
C
of the triangle, |
|
-
3x + 2y -
5 = 0
Tangents are perpendicular
since their slopes satisfy the condition, m1
=
- 1/m2. |
|
2x + 3y -
14 = 0,
C(1, 4) |
| |
| The triangle
ABC is right isosceles, whose area
A =
1/2 · AC 2
=
1/2 · Ö(22
+ 32)2
=
13/2 square units. |
|
|
|
|
|
|