Probability, probability of two independent events, probability of two dependent events

Probability

The probability of two independent events

The events are said to be independent if the occurrence of one event does not affect the probability of any of the others.

The probability that two independent events A and B both occur is given by

P ( A Ç B ) = P (A) · P (B)

The probability of any set of independent events occurring equals the product of their individual probabilities.

The probability of two dependent events

The events are said to be dependent if the occurrence of one event affects the outcome of the others.

The probability that two dependent events A and B both occur is given by

P ( A Ç B ) = P (A) · P (B|A) = P (B) · P (A|B)

Calculating probabilities, examples

Example: What is the probability when rolling a dice to get the result divisible by 2 or 3?

Solution: The probability that an event E will occur,

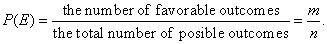If rolling a dice we get numbers, 2, 4 or 6, fulfilled is condition for the event A, and if we get numbers, 3 or 6, fulfilled is condition for the event B.

Notice that number 6 satisfy both events, so this outcome we should include in the event A or B, thus "or” probability of mutually exclusive events

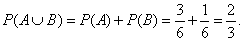Example: By rolling three dice at once find probability that the product of all three numbers that come up is divisible by 50.

Solution: The required condition (the product of all three numbers should be divisible by 50) will satisfy triples, events when three dice show up: 6, 5, 5 and 5, 5, 2.

To calculate the number of favorable outcomes, each of the triples brings, use the formula for permutations of

n elements (objects), some groups, r, s, t, . . . of which, are the same,

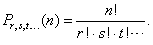So, each triple ( 6, 5, 5 and 5, 5, 2) gives

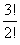permutations, where 3 stands for the three shown figures, two

of which are the same. Therefore,

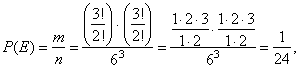where the total number of outcomes 6³equals the number of variations with repetition the three dies, with six sides each, show up.

Example: What is the probability that in two throws of a die the sum of the numbers that come up is 5 or product is 4?

Solution: Two throws of a die we can consider as one throw of two dice. So, the number of favorable outcomes, that the first event occurs (i.e., the sum of the numbers that come up is 5) is determined by pairs, the event E₁: (1, 4), (2, 3), (4, 1) and (3, 2).

The second event (product is 4) is determined by pairs, the event E₂: (1, 4), (2, 2), (4, 1).

Notice that pairs (1, 4) and (4, 1) appear in both events, so we should include them in the event E₁ or E₂.

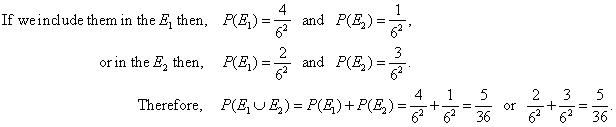Example: What is the probability that in four consecutive throws of a dice, come up four different numbers?

Solution:

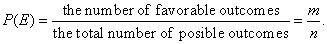The number of favorable outcomes m corresponds to the number of permuted combinations (or variations) of the subset with k = 4 elements (four throws of one die or one throw of 4 dice) out of the set of 6 elements (6 faces of the cube numbered from 1 to 6), i.e.,

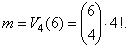The total number of possible outcomes n correspond to the number of permuted combinations with repetition of the subset with k = 4 elements out of the set of 6 elements, since each throw has 6 possible

outcomes,

Example: What is the probability that from a group of 3 men and 4 women we chose a three-member group which consists of one man and two women?

Solution: From the group of three men a one man we can choose on

ways,

and from four women we can choose two women on

ways,

so the number of favorable outcomes,

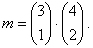From the group of seven people a three-member group can be chosen on n ways, i.e.,

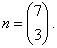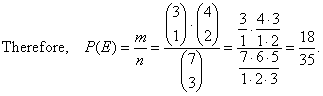Example: By rolling two dice at once find probability that the sum of numbers that come up is 6 or the sum is 9.

Solution: - The number of favorable outcomes that the event E₁ occurs is determined by pairs:

(1, 5), (2, 4), (3, 3), (4, 2) and (5, 1), the pairs whose sum is 6.

- The number of favorable outcomes that the event E₂ occurs is determined by pairs:

(3, 6), (4, 5), (5, 4) and (6, 3), the pairs whose sum is 9.

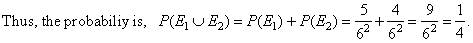Combinatorics and probability contents