|
| Sequences and
Series
|
|
Geometric sequence/progression |
|
General term of a geometric sequence
|
|
The sum of the first n terms of a finite geometric
sequence, geometric series |
|
Geometric sequences, examples
|
|
|
|
|
|
|
|
Geometric sequence or
progression
|
|
A sequence of numbers in
which the ratio r
of each two successive terms an /
an
-1
is constant or whose each term is r
times the preceding.
|
|
For example, in the
sequence 1, 3, 9, 27,
.
. . ,
each term is 3
times the preceding,
that is r
= 3.
|
|
Therefore,
a
geometric
sequence can be written as
|
|
a1,
a2, a3, a4,
. . . , an
-1,
an, . . .
or a1,
a1 · r, a1 · r2,
a1 · r3, . . . , an
-1,
an, . . .
|
|
where,
a2
= a1 · r,
|
|
a3 = a1 · r2,
|
|
a4 = a1 · r3,
and so on.
|
|
So,
the formula for the nth
term, or the general term of a
geometric sequence
is
|
|
|
| A
geometric
sequence is said to be convergent if -1
< r <
1 that
is,
an
approaches zero as n
becomes infinitely large thus, the limit of the sequence is 0. |
| An
infinite sequence that has no a finite limit is called a divergent
sequence. |
|
| The sum of the first n terms of a finite geometric
sequence, geometric series |
| The
sum of numbers in a geometric sequence we call the geometric series and
write, |
|
Sn = a1 + a2 + a3 +
. . . + an
-1 +
an, |
|
that is
Sn
= a1 + a1 · r + a1
· r2 + . . . + a1 · rn -2
+ a1 · rn -1, |
|
or
Sn
= a1 · (1 + r + r2
+ . . . + rn -2 +
rn -1) |
| thus, |
 |
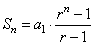the
sum of the first n terms of a finite geometric sequence or
series. |
|
| Recall
that by factoring binomial xn
-
yn
= (x
-
y) · (xn -1 +
xn -2y +
xn -3y2 +
. . . + xyn -2 +
y n -1)
|
|
so that, rn
-
1n
= (r
-
1) · (rn -1 +
rn -2 +
rn -3 +
. . . + r2
+ r + 1). |
|
| Or,
we can use following method to derive the same formula, |
|
Sn
= a1 + a1 · r + a1
· r2 + . . . + a1 · rn -2
+ a1 · rn -1, |
|
and
r · Sn
= a1 · r + a1 · r2
+ a1 · r3 + . . . + a1
· rn -1
+ a1 · rn, |
|
then r
·
Sn
-
Sn
= a1 · rn
-
a1
or
Sn
· (r
-
1) = a1 · (rn
-
1) => Sn
=
a1 · (rn
-
1) /
(r
-
1). |
|
| Geometric sequences, examples
|
| Example:
Find
the sum of the
first six terms of the geometric sequence 1, 3, 9, 27, 81, 243, 729,
. . .
|
|
Solution: Since,
a1
= 1, r
= 3
and n
= 6
|
|
we plug
these values into the formula for the first n
terms of a finite geometric sequence,
|
|
Sn
= [a1 · (rn
-
1)] / (r
-
1)
= [1
·
(36
-
1)] / (3
-
1)
= 728 / 2
= 364.
|
|
| Example:
Find
the first term a1
and the number of
terms n
in a geometric sequence
with the general term an
= 192, the sum
of the first n
terms Sn
=
381 and
the common ratio r
= 2. |
|
Solution: Using
the formulas for an
and Sn
we get the system of two equations in two unknown,
|
 |
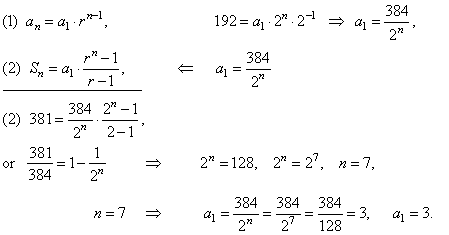| Therefore,
the geometric sequence is 3, 6, 12, 24, 48, 96, 192
. . .
|
|
| Example:
Write the geometric
sequence such that the sum of its first three terms is 21 and the
difference between the first and the second term is 12. |
|
Solution: Given
are the equations,
|
|
(1) a1 + a2 + a3
= 21
or a1
+ a1r + a1r2
= 21, a1
· (1 + r + r2)
= 21 |
| and
(2)
a1 -
a2
= 12
a1 - a1r
= 12,
a1
· (1 -
r)
= 12 |
 |
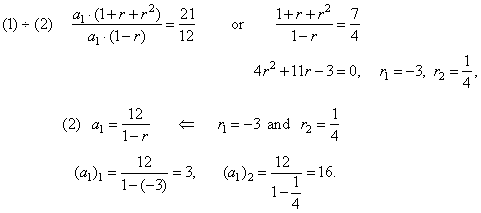| Thus,
the two geometric sequences satisfy the given conditions, |
|
(a1)1 = 3
and r1
= -3
give 3, -9,
27 |
|
(a1)2
= 16
and r2
= 1/4
give 16, 4, 1. |
|
|
|
|
|
