|
|
|
 Linear Inequalities
Linear Inequalities
|
|
Solving
inequalities |
|
Properties of
inequalities |
|
Examples
of solving single linear inequalities |
|
Solving
compound (double) inequalities |
|
|
|
|
|
|
|
| Linear Inequalities
|
| A linear inequality
is one that can be reduced to the standard form
ax +
b
> 0 where a,
b
Î
R,
and where other inequality signs like <
, > and
<
can appear. |
| Solving
inequalities |
| The solutions to an inequality are all values of
x
that make the inequality true. Usually the answer is a range of
values of x
that we plot on a number line. |
| We
use similar method to solve linear inequalities as
for solving linear equations: |
| -
simplify both sides, |
| -
bring all the terms with the variable on one side and the
constants
on the other side, |
| - and then multiply/divide both sides by the
coefficient of the variable to get the solution while applying following properties: |
|
| Properties of
inequalities |
| 1. Adding
or subtracting the same quantity from both sides of an
inequality will not change the direction of the inequality sign. |
| 2. Multiplying
or dividing both sides of an inequality by a positive number leaves the
inequality symbol unchanged. |
| 3.
Multiplying or dividing both sides of an inequality
by the same negative number, the sense of the inequality changes,
i.e., it reverses the direction of the inequality sign. |
|
| Examples
of solving single linear inequalities |
| Solve
each of the following inequalities, sketch the solution on the
real number line and express the solution in interval notation. |
|
Example:
3(x -
2) >
-2(1-
x)
|
|
Solution:
3x -
6
>
-2
+
2x |
|
x > 4 |
|
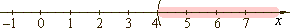 |
|
interval
notation
(4, oo) |
|
|
| The
open interval (4,
oo) contains all real numbers between given endpoints, where round
parentheses indicate exclusion of endpoints. |
|
| Example:
|
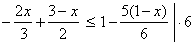 |
|
Solution: -4x
+
9 -
3x
<
6 - 5
+
5x |
|
-12x
< -8 |
|
x
> 2/3 |
|
|
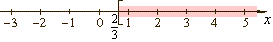 |
| interval
notation |
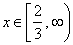 |
|
|
| The
half-closed (or half-open) interval
contains all real numbers between given endpoints, where the
square bracket indicates inclusion of the endpoint 2/3 and round
parenthesis indicates exclusion of infinity. |
|
|
Example:
(x
- 3)
· (x
+ 2)
> 0 |
| Solution:
The factor
x
- 3
has the zero at x
= 3, is negative for x
< 3
and is positive for x
> 3,
and |
|
the factor
x
+ 2
has the zero at x
= -2,
is negative for x
< - 2
and is positive for x
> -2, |
| as
is shown in the table |
| x |
-
oo |
increases |
-2 |
increases |
3 |
increases |
+
oo |
| x
+ 2 |
|
- |
0 |
+ |
+ |
+ |
|
| x
- 3 |
|
- |
- |
- |
0 |
+ |
|
| (x
- 3)(x
+ 2) |
|
+ |
0 |
- |
0 |
+ |
|
|
|
| Thus,
the given inequality is satisfied for -
oo
< x
<
- 2
or 3
<
x
< +
oo |
|
in the interval notation (
- oo
, -2
]
U [
3, +
oo
) |
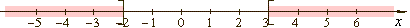 |
|
| Solving
compound (double) inequalities |
| Use the same procedure to solve a compound inequality as for solving single inequalities. |
| Example:
-4
< 2(x
- 3)
< 5 |
|
|
Solution: We want the x alone as middle term and only constants in the two outer terms. Remember,
while simplifying given compound inequality, the operations that we apply to a middle term we
should also do to the both left and right side of the inequality. |
|
|
|
|
|
|
|
| Example: |
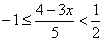 |
|
|
Solution: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| College
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |