|
|
|
|
Real
Numbers |
 The set of real
numbers
The set of real
numbers |
 Rational numbers Rational numbers |
|
Decimal representation of rational
numbers or fractions
|
|
Expanded form of decimal number,
decimal fractions
|
|
Terminating decimals
|
|
Recurring decimals (Infinite decimals, period) |
|
Purely recurring decimals |
|
Mixed recurring decimals
|
|
Converting decimal number to a
fraction |
|
Converting
terminating decimal to a fraction |
|
Converting the purely recurring decimal
to a fraction |
|
Converting the mixed recurring decimal
to a fraction |
|
Exponential or
scientific notation of decimal numbers
|
|
Converting
from a number to scientific notation |
|
Converting
from scientific notation to a decimal number |
|
|
|
|
|
|
| The set of real
numbers |
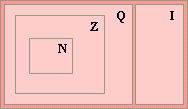
| The set of
real numbers, denoted R,
is
the set of all rational and irrational numbers, R =
Q U I.
The real numbers or the
reals are either rational or
irrational and are intuitively defined as numbers that are in one-to-one correspondence with the points on an infinite line, the
number
line or the real line. |
 |
|
|
| The set of
natural numbers |
|
N = {1, 2, 3,
. . . , n,
n
+ 1, . . . }, the positive integers used for counting. |
| The
set of whole numbers |
|
N0
= {
0, 1, 2, 3, . .
. }, is just like the set of natural numbers except that it also
includes zero. |
| The set of integers |
|
Z
= {
. . . , −3, −2,
−1,
0, 1, 2, 3, . . . }, consists of all natural numbers, negative whole numbers and
zero. This means that the set of natural numbers is a subset of
integers, i.e., N
is a subset of
Z. |
| The set of
rational numbers |
|
Q
= {
a/b
| a,
b
Î Z,
b is
not
0 }, is the set of all proper and improper fractions. That is, a ratio or quotient of two
integers a
and b, where
b
is not zero. |
| All integers are in this set since every integer a
can be expressed as the fraction a/1
= a.
Thus, the set of all natural numbers
N is proper subset of integers
Z
and the set of integers is proper subset of the set of rational
numbers, N is proper subset of
Z
is proper subset of
Q.
Rational numbers can be represented as integers, fractions, terminating decimals and recurring or repeating decimals. |
| The set of irrational numbers, denoted I, is the set of numbers that
cannot be written as ratio of two |
| integers.
An irrational number expressed as a decimal never repeat or terminate. The irrational numbers are precisely those numbers whose decimal expansion never ends and never enters
a periodic pattern, such as 0.1020030004..., p,
Ö2, Ö3, or any root of any natural number that is not a perfect root is an irrational number.
|
|
|
Rational numbers
|
| Decimal representation of rational
numbers or fractions
|
| In order to convert a rational number represented as a fraction into
decimal form, one may use long division. |
| By dividing the numerator
by the denominator we get a terminating or a
recurring decimal. |
| If the final remainder is 0 the quotient is a whole number or a finite
or terminating decimal, i.e. a decimal with a limited number of digits after the decimal point. |
|
|
|
|
| Sometimes when dividing, the division will never stop as there is
always a remainder. |
| These fractions convert to a recurring,
(periodic or infinite) decimals, and they have an unlimited number
of digits after the decimal point. |
|
|
|
|
| A rational number is either a terminating decimal or recurring
decimal. |
| We can determine which fraction will convert to terminating
decimal and which to recurring decimal only if the given fraction is
expressed in its lowest terms, that is, when its numerator and the
denominator have no common factor other than 1. |
|
| Expanded form of decimal number,
decimal fractions
|
| The integer and fractional parts of a decimal number are separated
by a decimal point. |
| Converting decimals to fractions
involves
counting the number of places to the right of the decimal point. |
| This
will give the corresponding place value, which then determines the
number of zeros that will be used in forming the denominator. |
| The
numerator of the fraction equivalent is the number without the decimal point, and the denominator is 1 followed by the number of
zeros corresponding to the number of decimal places. |
|
|
|
|
| Terminating decimals
|
| The
irreducible fractions, i.e., the vulgar fractions in lowest terms
whose the only prime factors in a denominator are 2 and/or 5
can be converted to terminating decimals.
|
| That is, the terminating
decimals represent rational numbers whose fractions in the lowest
terms are of the form
a/(2n
· 5m). |
|
| Examples: |
|
 |
| |
|
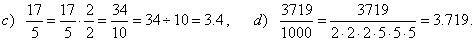 |
|
|
| Recurring decimals (Infinite decimals, period) |
| Purely recurring decimals |
| The irreducible fractions, i.e., the vulgar fractions in lowest terms
whose prime factors in the denominator are other than 2 or 5, that is,
the prime numbers from the sequence (3, 7, 11, 13, 17, 19, ...) convert to the
purely recurring decimals, i.e., the decimals which
start their recurring cycle immediately after the decimal point. |
|
| Examples: |
|
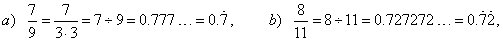 |
|
|
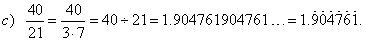 |
|
|
| Mixed recurring decimals
|
| The irreducible fractions, i.e., the vulgar fractions in lowest terms
whose denominator is a product of 2's and/or 5's besides the prime
numbers from the sequence (3, 7, 11, 13, 17, 19, ...) convert to the
mixed recurring decimals, i.e., the decimals that have some extra
digits before the repeating sequence of digits. |
| The repeating
sequence may consist of just one digit or of any finite number of
digits. The number of digits in the repeating pattern is called the
period. All recurring decimals are infinite decimals. |
|
| Examples: |
|
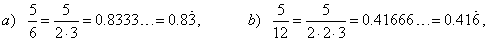 |
|
|
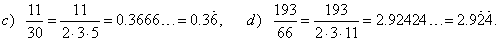 |
|
|
| All fractions can be written either as terminating decimals or as
recurring/repeating decimals. |
|
| Converting decimal number to a
fraction |
| Converting
terminating decimal to a fraction |
| Every terminating decimal and recurring decimal can be
converted to a fraction a/b,
a Î
Z,
b Î
N. |
|
| Examples: |
|
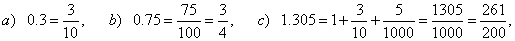 |
|
|
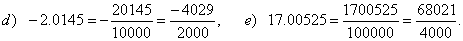 |
|
|
| Converting the purely recurring decimal
to a fraction |
| When converting the purely recurring decimal less than one to
fraction, write the group of repeating digits to the numerator, and to
the denominator of the equivalent fraction write as much 9’s as is
the number of digits in the repeating pattern.. |
|
| Examples: |
|
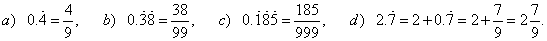 |
|
|
| Converting the mixed recurring decimal
to a fraction |
| When converting the mixed recurring decimal less than one to
fraction, write the difference between the number formed by the
entire sequence of digits, including the digits of the recurring part,
and the number formed only by the digits of the non-recurring pattern to its numerator.
|
| To the denominator of the equivalent
fraction write as much 9’s as is the number of digits in the repeating
pattern and add as much 0’s as is the number of digits in the non-recurring pattern. |
|
| Examples: |
|
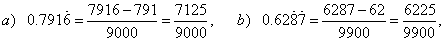 |
|
|
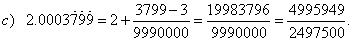 |
|
|
|
Exponential or
scientific notation of decimal numbers
|
| Exponential
or scientific
notation is used to express very large or very small numbers. |
| A
number in scientific notation is written as the product of a
number (the coefficient) and a power of 10 (the exponent), i.e., |
|
coefficient ´
10exponent |
| The
coefficient should have exactly one non-zero digit to the left of the decimal point. The
exponent indicates, how many places the decimal point was moved to
the left or to the right. If the decimal point was moved to the
left, the exponent is positive, if moved to the right the
exponent is negative. |
| Converting
from a number to scientific notation |
| Examples: |
|
a)
302,567,908 = 3.02567908 · 108 b)
0.000040635 = 4.0635 · 10−5. |
|
|
|
| Converting
from scientific notation to a decimal number |
| Examples: |
|
a)
2.09085 · 107 = 20908500
b)
7.81 · 10−5
= 0.0000781 |
|
|
|
|
|
|
|
|
|
|
|
|
| College
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved |