|
|
| Rational Expressions
|
 Simplification of rational expressions, reducing to lowest
terms
Simplification of rational expressions, reducing to lowest
terms
|
 Addition and subtraction of rational
expressions
Addition and subtraction of rational
expressions
|
|
|
|
|
|
|
| Simplification of rational expressions, reducing to lowest
terms
|
| A
rational expression is a fraction of which the numerator and the
denominator are polynomials. |
| A
rational expression is reduced to lowest terms if all common
factors from the numerator and denominator are cancelled. |
| To
reduce a rational expression to lowest terms first factorize
both the numerator and denominator as much as possible then
cancel common factors, i.e., divide their numerator and
denominator by common factors. |
|
| Examples:
Reduce the following
rational expression to lowest terms. |
| |
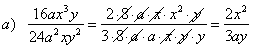 |
| |
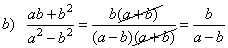 |
| |
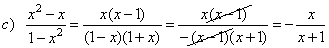 |
| |
factoring
out the minus sign, |
|
or |
|
|
| |
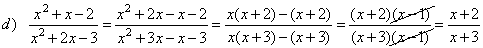 |
| |
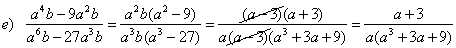 |
| |
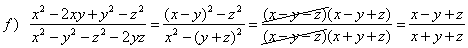 |
|
|
| Examples:
Reduce or simplify the following
rational expression to lowest terms. |
|
|
|
| Addition and subtraction of rational
expressions
|
| To add or subtract two fractions with
the same denominator, add or subtract the numerators and write the sum over the common denominator. |
| To add or subtract fractions with different
denominators: |
| First find
the least common denominator (lcd -the smallest number that can be
divided by each denominator). |
| Write equivalent fractions using this
denominator. Then add or subtract the fractions. |
| The
process for rational expressions is identical. |
|
| Examples:
Perform the indicated
operations and reduce the answer to lowest terms. |
|
|
|
|
|
|
|
|
|
|
|
|
| College
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |