|
| Probability |
|
|
|
Probability
definition, terms
and notation |
|
Sample space, event |
|
Probability formula |
|
The probability of
mutually exclusive events |
|
The probability of not
mutually exclusive events |
|
Calculating
probabilities, examples |
|
|
|
|
|
|
| Probability
definition, terms
and notation |
| The
probability is defined as a measure of the degree of confidence in the
occurrence of an event, measured on a scale from 0 (impossibility) to 1
(certainty), expressed as the ratio of favorable outcomes of the event
to the total number of possible outcomes. |
| Thus,
the probability of an event
A
occurring, |
|
|
| where, |
0
<
P(A)
<
1, |
so
that, |
P(not
A) = 1 -
P(A) |
and |
P(A)
= 1 -
P(not A). |
|
|
| The set of all possible outcomes
called the sample
space, |
S
= A
U
not A. |
|
|
|
| The probability of
mutually exclusive events |
| The probability of mutually exclusive events, either
A
or B
(or both) occurring is |
|
|
| The
probability of either events A
or B
(or both), occurring is written
P( A
U B ). |
|
| The probability of not
mutually exclusive events |
| The probability of
not mutually exclusive events, either A
or B (or
both) occurring is |
| |
P( A
U B )
= P(A) + P(B) -
P(
A Ç B
) |
|
|
| The
probability of events A
and B
both occurring is written P(
A Ç B
). |
|
|
| Calculating
probabilities, examples |
| Example:
What is the probability when rolling a die to get the result divisible by 2 or 3?
|
| Solution:
The probability that an event
E
will occur, |
 |
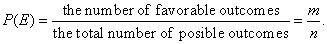| If rolling a die we get numbers, 2, 4 or 6, fulfilled is condition for the event
A,
and if we get numbers, 3 or 6, fulfilled is condition for the event B.
|
| Notice that number 6 satisfy both events, so this outcome we
should include in the event A
or B,
thus "or” probability
of mutually exclusive events |
 |
|
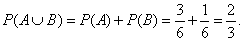| Example:
By rolling three dice at once find probability that the product of all three numbers that come up is divisible by 50.
|
| Solution:
The required condition (the product of all three numbers should be divisible by 50) will satisfy
triples,
events when three dice show up: 6, 5, 5 and 5, 5, 2. |
| To calculate the number of favorable outcomes, each of the triples brings, use the formula for
permutations of |
| n
elements (objects), some groups, r,
s,
t, . . . of which, are the
same, |
 |
|
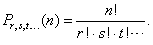| So, each triple
( 6, 5, 5 and 5, 5,
2) gives |
 |
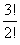permutations,
where 3 stands for the three shown figures, two |
|
| of which are the
same. Therefore, |
 |
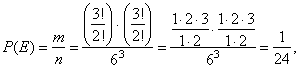| where
the total number of outcomes 63
equals the
number of variations
with repetition the three
dice, with six sides each, show up. |
|
| Example:
What is the probability that in two throws of a dice the sum of the numbers that come up is 5 or product is 4?
|
| Solution:
Two throws of a
dice we can consider as one throw of two dice. So, the number of favorable
outcomes,
that the first event occurs (i.e., the sum of the numbers that come up is 5) is determined by pairs,
the event E1:
(1, 4), (2, 3), (4, 1) and (3, 2). |
| The second event (product is 4) is determined by pairs,
and the event E2:
(1, 4), (2, 2), (4, 1). |
| Notice that pairs (1, 4) and (4, 1) appear in both events, so we should include them in the event
E1
or E2. |
 |
|
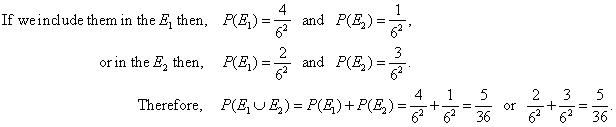| Example: What is the probability that in two throws of a
dice the sum of the numbers that come up is 7 or product is 10?
|
| Solution:
The number of favorable outcomes that:
- the event E1
(the sum of the numbers is 7) occurs is determined by pairs:
(1, 6), (2, 5), (3, 4), (6, 1), (5, 2), (4, 3), |
|
- the event E2
(the product of the shown numbers is 10) occurs is determined by pairs: (2,
5) and (5, 2). |
| Since the pairs (2, 5) and (5, 2) are already contained in the event
E1
then, the probability is |
 |
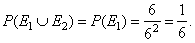| We get the same result by counting the two pairs in the event
E2
(but then, we don't count them in
the E1), so |
 |
|
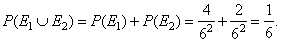| Example: In a box there are 9 balls numbered from 1 to 9. If we draw from the box two balls at once, what is the probability
that the sum of both numbers is odd and less than 8?
|
| Solution:
According to stated conditions about the number of favorable outcomes
m
will give us the following pairs of numbered balls: (1, 2), (1, 4), (1, 6), (2, 3), (2, 5), and (3,
4). |
| The total number of possible outcomes is equal to the number of the
combinations of the subset with
k =
2 elements out of the set of
n = 9 elements, i.e., |
 |
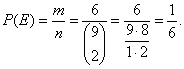