|
|
|
|
The Binomial Theorem
|
The binomial theorem, sigma notation
and binomial expansion
algorithm |
|
The
binomial theorem and binomial expansion algorithm examples |
|
|
|
|
|
|
|
The binomial theorem, sigma notation
and binomial expansion
algorithm |
| The
theorem that shows the form of the expansion of any positive integral
power of a binomial (a
+ b)n
to a polynomial with n
+ 1 terms, |
 |
|
|
|
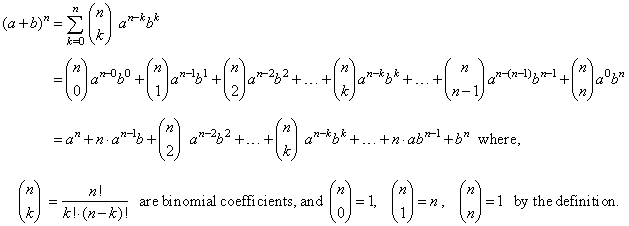The
binomial theorem and binomial expansion algorithm examples
|
|
|
|
| Example: Find
the 4th term of the binomial
expansion (a - x)5. |
|
|
| Or,
we can use the formula to find (k
+ 1)th
term. |
|
|
| Since, n =
5
and k
+ 1 = 4 =>
k
=
3
then by plugging these values into |
 |
|
 |
|
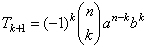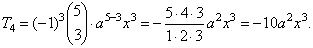| Example: Find
the middle
term of the binomial
expansion |
 |
|
|
|
|
| Example: Find
the 7th term of the binomial
expansion |
 |
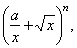if the coefficient of the third
term |
|
| relates
to the coefficient of the second term as 9 : 2. |
|
|
|
| Example:
Which term of the binomial
expansion |
 |
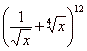is missing x? |
|
|
|
| To
fulfill the required condition, the exponent of x
must be zero, therefore |
 |
