|
| Conic
Sections |
|
|
|
|
Ellipse
and Line
|
Tangents to an ellipse from a
point outside the ellipse - use of the tangency condition
|
|
Construction of tangents from a point outside the ellipse
|
|
Ellipse and line examples
|
|
|
|
|
|
|
| Tangents to an ellipse from a
point outside the ellipse - use of the tangency condition
|
| Coordinates of the point
A(x, y), from which we draw tangents to an ellipse, must satisfy
equations of the tangents, y
= mx + c and their slopes and intercepts,
m and
c, must satisfy the
condition of tangency therefore, using the system of equations, |
|
(1) y = mx + c
<=
A(x, y) |
|
(2) a2m2 + b2
= c2
determined are equations of the tangents from a point A(x, y)
outside the ellipse. |
|
|
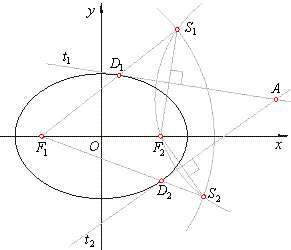
| Construction of tangents from a point outside the ellipse
|
| With
A
as center, draw an arc through F2, and from
F1
as center, draw an arc of the radius 2a. Tangents are |
|
then the perpendicular bisectors of the line segments,
F2S1 and
F2S2.
|
|
We can also draw tangents as lines through A
and the intersection points of the segments F1S1 and
F1S2
and the ellipse. |
| Thus, these intersections are the tangency points
of the tangents to the ellipse. |
| Explanation of the construction lies at the fact that, |
|
F1S1 =
F1D1 +
D1S1 =
F1D1 +
D1F2 = 2a
|
|
according to the definition of the ellipse, as well as
the point A
is equidistant from points F2 and
S1,
since the point S1
lies on the arc drawn from A
through F2.
|
|
 |
|
|
| Ellipse and line examples
|
| Example: Determine equation of the ellipse which the line
-3x +
10y = 25 touches at the point
P(-3,
8/5). |
| Solution:
As the given line is the tangent to the ellipse,
parameters, m
and c
of the line must satisfy the tangency condition, and the point P
must satisfy the equations of the line and the ellipse, thus |
 |
|
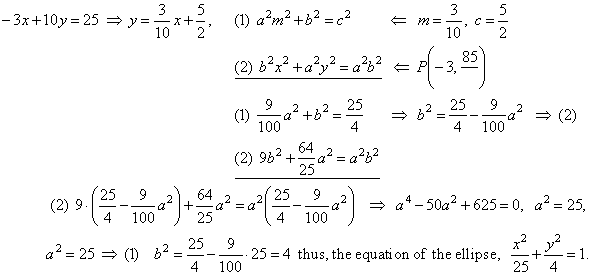| Example:
At which points
curves, x2
+ y2 = 8 and
x2
+ 8y2 = 36, intersect? Find the angle between two
curves. |
| Solution:
Given curves are the circle and the
ellipse. The solutions
of the system of their equations determine the intersection points, so |
 |
|
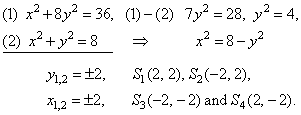Angle between two curves is the angle between
tangents drawn
to the curves at their point of
intersection.
|
|
The tangent to the circle at the intersection
S1,
|
|
S1(2,
2) =>
x1x
+ y1y =
r2,
2x +
2y = 8
|
|
or tc
::
y =
-
x
+ 4
therefore, mc
= -1.
|
|
The tangent to the
ellipse at the intersection
S1,
|
|
 |
|
 |
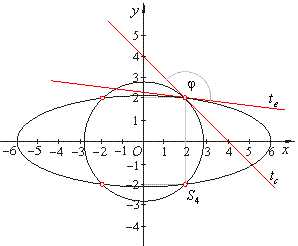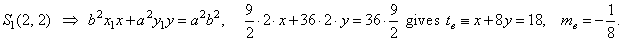| The angle between the circle and the ellipse,
|
 |
|
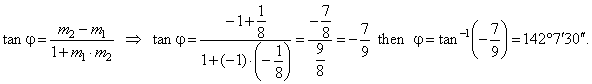| Example:
Find the equations of the common tangents of the curves
4x2
+ 9y2 = 36 and
x2
+ y2 = 5. |
| Solution: The common tangents of the ellipse and the circle
must satisfy the tangency conditions of these curves, thus |
|
|
 |
|
|
|
|
|
|
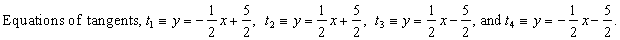