|
| Conic
Sections |
|
|
|
|
Circle |
 General equation of a circle with the center
S(p, q) - translated circle
General equation of a circle with the center
S(p, q) - translated circle |
|
The
equation of the circle, example |
|
Equation of the circle with the
center at the origin O(0, 0)
|
 Circle through three points
Circle through three points
|
|
The
equation of the circle
through three points,
example |
|
|
|
|
|
|
| Circle |
| General equation of a circle with the center
S(p, q)
- translated circle |
| A circle with the center
at the point S(p,
q) and radius r is a set of all points P(x,
y) of a plane to whom the |
| distance from the center,
SP
= r
or |
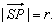 |
|
|
|
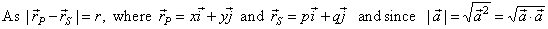 |
 |
| is
the general equation
of a circle with the
center S(p,
q). |
|
|
| Equation of the circle with the
center at the origin
O(0,
0),
|
 |
|
|
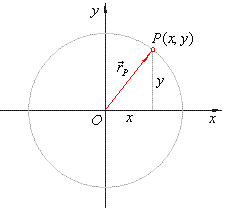 |
|
|
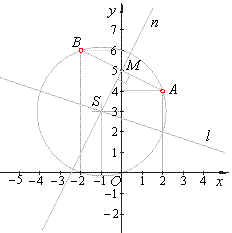
| Example: A circle passes through points A(2, 4) and
B(-2, 6) and its center lies on a line
x + 3y
-
8 = 0. |
| Find equation of the circle. |
| Solution:
The intersection of the chord AB
bisector and the given line is the center S
of the circle, since the
bisector is normal through the midpoint M, then |
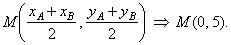 |
| As the bisector is perpendicular to the line AB |
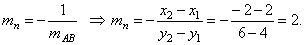 |
| Equation of the bisector |
| M(0,
5) and
mn = 2
=>
y
-
y1 = m( x -
x1), |
| gives
y
-
5 = 2(x -
0)
or -2x
+ y
-
5 = 0. |
|
 |
|
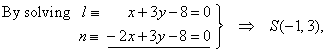 |
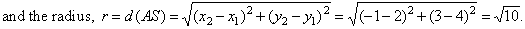 |
| So,
the equation of the circle, (x
-
p)2 + (y -
q)2 = r2
=>
(x +
1)2 + (y -
3)2 = 10. |
|
| Circle through three points
|
| A circle is uniquely determined by three points not lying on the same line. If given are points,
A,
B
and C
then the intersection of any pair of the perpendicular bisectors of the
sides of the triangle ABC is the center of the circle. |
| Since all three points lie on the circle, their coordinates must
satisfy equation of the circle |
| (x
-
p)2 + (y -
q)2 = r2. |
| Thus, we obtain the system of three equations in three unknowns
p,
q
and r. |
| Subtracting second equation from first and then third from first
we obtain two equations in two unknowns p and
q. |
| Solutions of that system plug into any of three equations to
get r. |
|
 |
|
|
| Example:
Find equation of a circle passing through three
points, A(-2,
-6),
B(5, -7)
and C(6, 0). |
| Solution:
The coordinates of the points, A,
B
and C
plug into equation (x
-
p)2 + (y -
q)2 = r2,
|
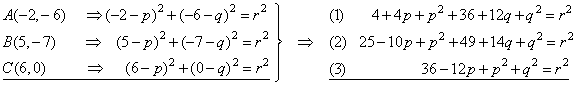 |
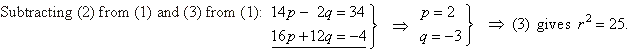 |
| Thus,
the equation of the circle through points A,
B
and C,
(x
-
2)2 + (y +
3)2 = 25. |
|
|
|
|
|
|
|