|
|
The limit of a sequence,
theorems |
 Sufficient condition for convergence of a sequence
Sufficient condition for convergence of a sequence |
|
The Cauchy criterion (general principle of convergence) |
 Some
important limits
Some
important limits |
|
|
|
|
|
|
| Sufficient condition for convergence of a sequence
- The Cauchy criterion (general principle of convergence) |
| A
sequence of real numbers, a1,
a2,
. . . ,
an,
. . .
will have a finite limit value or
will be convergent if for no matter
how small a positive number e
we take there exists a term an
such that the distance between that term
and every term further in the sequence is smaller than e,
that is, by moving further in the sequence the
difference between any two terms gets
smaller and smaller. |
| As
an + r,
where
r = 1, 2, 3,
. . . denotes any term that follows an,
then |
| |
an + r -
an
| < e
for all n >
n0(e),
r
= 1, 2, 3,
. . . |
| shows
the condition for the convergence of a sequence. |
| If
a sequence {an}
of real numbers (or points on the real line) the distances between which
tend to zero as their
indices tend to infinity, then {an}
is a Cauchy sequence. |
| Therefore,
if a sequence {an}
is convergent, then {an}
is a Cauchy sequence. |
|
| The Cauchy criterion
or general principle of convergence,
example |
| The
following example shows us the nature of that condition. |
| Example: We
know that the sequence 0.3,
0.33,
0.333,
. . . converges to the number 1/3
as |
| 1/3
= 0.33333
. . . . Let
write the rule for the nth
term, |
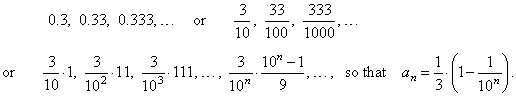 |
|
If we go along the sequence far enough, say to the 100th term, i.e., the
term with a hundred 3's in the fractional
part, then the difference between that term and every next term is equal
to the decimal fraction with the
fractional part that consists of a hundred 0's followed by 3's on the
lower decimal places, starting from the
101st decimal place. That is, |
 |
| Therefore,
the absolute value of the difference falls under |
 |
|
| Then,
if we go further along the sequence and for example calculate the
distance between the 100000th term |
| and the following
terms, the distance will be smaller than |
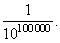 |
|
| Hence,
since we can make the left side of
the inequality |
an + r -
an
| < e as
small as we wish by choosing n
large enough, then all terms that follow an
(denoted an + r,
r = 1, 2, 3,
. . . ), infinitely many
of
them, lie in
the interval
of the length 2e symmetrically
around the point an.
Outside of that interval there is only
a finite number of terms. That is, |
| -
e <
an + r -
an
< + e for all
n >
n0(e),
r
= 1, 2, 3,
. . . |
|
or an
-
e <
an + r < an
+ e. |
| So,
the
terms of the sequence, starting from the (n +
1)th term, form the
infinite and bounded sequence of numbers
and so, according to the above
theorem, they must have at least one cluster point that lies in that
interval. But they cannot have more than one cluster point since all
points that follow the nth term lie inside the interval
2e length of
which is arbitrary small, if n
is already large enough, so that any
other cluster point will have to be outside of that interval. |
| Thus,
the
above theorem simply says that if a sequence converges, then the terms of the sequence
are getting closer and closer to each
other as shows the example. |
|
| Some
important limits |
| (1)
Let examine convergence of the sequence given by an
= | a |n |
|
a) if | a |
> 1 then we can write |
a | = 1 + h,
where h
is a positive number. |
| So,
by the binomial theorem |
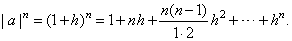 |
| If
we drop all terms beginning from the third that are all positive since
the binomial coefficients are natural numbers, if n > 2
and h
> 0, the right side become smaller, so obtained is the Bernoulli's
inequality |
| (1 + h)n
> 1 + nh,
n > 2. |
| When
n
®
oo
then 1 + nh
tends to the positive infinity too, since we can make 1 +
nh
greater than any |
| given positive number N,
if only we take |
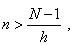 |
therefore will even more tend to infinity
| a |n
which is |
|
| greater.
Thus, |
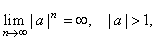 |
or |
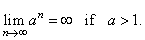 |
|
|
|
| b) if
0 < | a | < 1 then we can write |
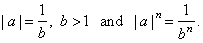 |
|
|
| Since b
> 1 then |
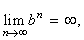 |
such that | a |n
< e
whenever |
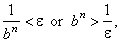 |
however small e is, |
|
| this
inequality can be satisfied by choosing n
large enough. Therefore, |
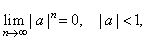 |
or |
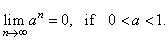 |
|
|
|
| (2) Let examine convergence of the sequence given by |
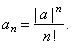 |
|
| The
sequence |
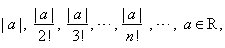 |
the n-th
term of which we can write as |
|
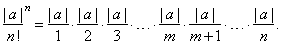 |
| For
every | a | >
1 there exists a natural number m
such that m <
| a | < m + 1
and n
> m
then |
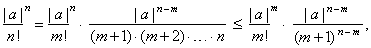 |
| since |
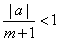 |
it follows that an
® 0
or we write |
|
|
|
|
| (3) Let examine convergence of the sequence given by |
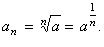 |
|
|
a) If a
> 1 then the sequence |
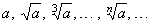 |
is decreasing, that is |
|
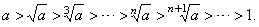 |
| Let |
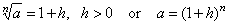 |
then by the Bernoulli's
inequality a
> 1 + nh
so that |
|
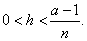 |
Since the numerator a
-
1 is fixed number then,
if n ® 0
then h ® 0
too, therefore |
|
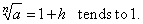 |
So we
can write |
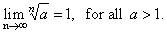 |
|
|
|
b) If
0 < a < 1 then the sequence |
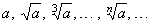 |
is increasing, that is |
|
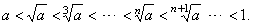 |
| For
example, |
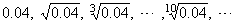 |
|
|
|
| If
we write |
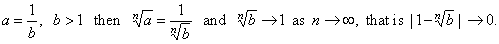 |
|
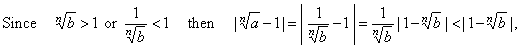 |
| so it
follows that |
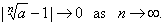 |
Therefore,
|
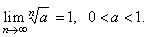 |
|
|
|
c) If
a = 1 then |
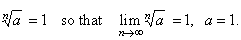 |
|
|
|
| Since
in all three cases above, a), b) and c) we've got the same result,
then we can write |
|
|
|
|