|
| Integral
calculus |
|
|
|
The
indefinite integral |
 Integrating
rational functions
Integrating
rational functions
|
|
Use
of the
partial fraction decomposition to integrate a proper rational
function
|
|
Use
of the
partial fraction decomposition to integrate a proper rational
function examples
|
|
|
|
|
|
|
|
|
|
|
|
Integrating
rational functions
|
|
Recall
that a rational function is a ratio of two polynomials
written Pn(x)
/ Qm(x).
|
|
To
integrate a rational function
|
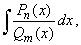
|
|
in
case n >
m, that is, if the
degree of P
is greater than or equal to degree of Q,
we first divide Pn(x)
by Qm(x)
to obtain the sum of the polynomial Pn
-
m(x)
and a proper or simple rational function.
|
|
Then,
we integrate proper rational function using decomposition of rational function
into a sum of partial fractions.
|
|
|
|
Use
of the
partial fraction decomposition to integrate a proper rational
function
|
|
Any
polynomial with real coefficients can be factored uniquely into a
product of its lading coefficient, linear
factors
of the form (x
-
c)
that
correspond to its real roots, and
irreducible quadratic
polynomials that
correspond
to pairs of conjugate complex roots.
|
|
Therefore,
to
represent a proper rational function as a finite sum of terms we
factor the polynomial Q
in the
denominator
into powers of distinct linear terms and/or powers of distinct
irreducible quadratic polynomials, i.e., which do not have real roots.
Thus,
|
|
-
if the factors of
Q
in the denominator are
of the form (x
-
c)
then the partial fractions will be of the form
|
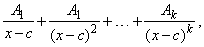
|
|
where
c
is a real root of order k
and A1,
A2,
. . . , Ak
are unknown constants.
|
|
-
If
the factors of Q
are
irreducible quadratic polynomials
|
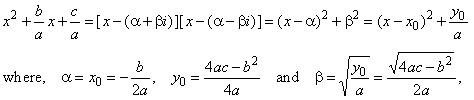
|
|
of
order k then,
the partial
fractions will be of the form
|
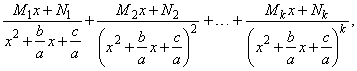
|
|
where
M1,
M2,
. . . , Mk
and N1,
N2,
. . . , Nk
are unknown constants.
|
|
Note
that the leading coefficient a
and the vertical translation y0
of a quadratic polynomial should be of the same
sign the quadratic to have pair of conjugate complex roots a
±
bi.
|
|
|
|
Use
of the
partial fraction decomposition to integrate a proper rational
function examples
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Calculus contents
F |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |