Integral calculus
      The indefinite integral
      The indefinite integrals containing quadratic polynomial (trinomial)
         The indefinite integrals containing quadratic polynomial, examples
  55.  Evaluate
We solve given integral by separating the derivative of the quadratic polynomial in the numerator, thus
solution: 
therefore, the solution of I2 depend on the leading coefficient a and the vertical translation  y0, i.e.,
a )   if 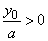then,  
b )  if 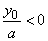then,  
 
   c )  if   y0 = 0  then,
 
  56.  Evaluate
Solution: 
The integrand function to be real, the quadratic polynomial in the denominator must be positive, therefore
 a )   if  a > 0  and   y0 is not 0  then 
 b )   if  a < 0  and   y0 > 0  then 
 c )   if  a > 0  and   y0 = 0  then 
  57.  Evaluate
 
Use similar methods to solve this integral as in the preceding example. Hence, the solutions depend on the sign of the leading coefficient a and the sign or the value of the vertical translation y0.
Example:  57 a )  Evaluate
 
Let solve given integral by separating the derivative of the quadratic polynomial in the numerator.
Solution: 
  58.  Evaluate
Use the substitution  mx + n = 1/ t .
Example:  58 a )  Evaluate
Solution: 
  59.  Evaluate
Solution:
The integrand function to be real, the quadratic polynomial must be positive, therefore
 a )   if  a > 0  and   y0 is not 0  then
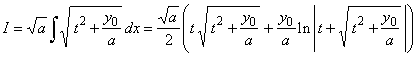
see the solutions of the integrals, example 31 and 36. By using above substitutions 
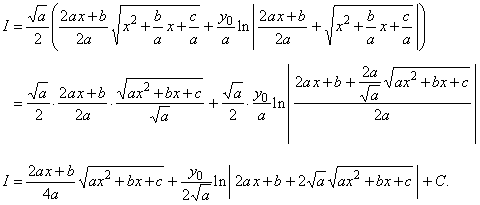
Note that the sign of the vertical translation y0 affects the solution, i.e., changes the sign of its second term.
 b )   if  a < 0  and   y0 > 0  then 
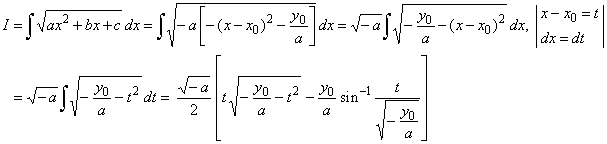
see the solution of the integral example 8 above. After applying the substitutions
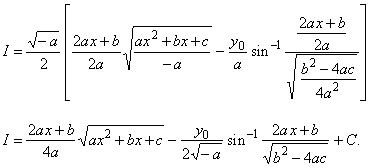
Calculus contents F
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.