|
| Integral
calculus |
|
|
|
 Differentiation
and integration of infinite series
Differentiation
and integration of infinite series
|
|
Differentiation
and integration of infinite series examples
|
|
|
|
|
|
|
|
|
|
|
|
Differentiation
and integration of infinite series
|
|
If
f (x)
is represented by the sum of a power series
|
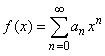
|
|
with
radius of convergence r
> 0 and -
r < x < r,
then the function has the derivative
|
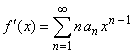
|
|
and
the function has the integral
|
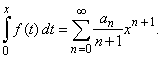
|
|
Thus,
a power series can be differentiated
and integrated term by term while the radius of convergence
remains
the same, with only (possible) exception at the endpoints of the
interval of convergence.
|
|
|
|
Differentiation
and integration of infinite series examples
|
|
Example:
Represent the f
(x) = arctan x
or f
(x) = tan -1
x,
by a power series.
|
| Solution:
Since |
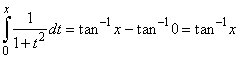 |
|
|
thus, we should integrate the series
|
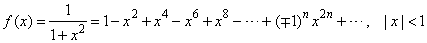 |
| Let
write down the initial sequence of nth
order polynomials that describe the function inside the interval of convergence
-1
< x < 1, |
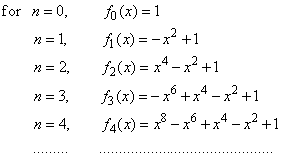 |
| Since
every polynomial above is missing the preceding odd degree term, their
coefficient an-1
= 0 |
| thus, the coordinates
of translations |
|
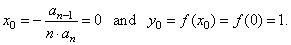 |
|
|
| Therefore,
the polynomials that describe the function
all are
source polynomials of even degree translated in the
direction
of the y
axis by y0
= 1, as is shown in the picture below.
|
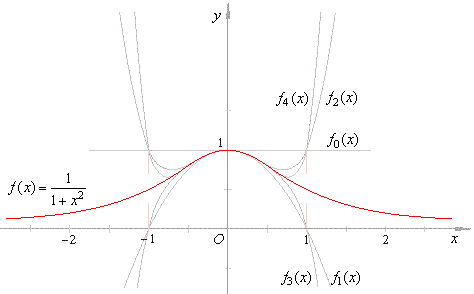
|
| The above graph
shows that all evenly indexed polynomials (with the positive
leading coefficient) intersect at (-1,
1) and (1,
1) while all polynomials with odd
indexes, with the negative leading coefficient, intersect at (-1,
0) and (1,
0). |
| Thus, they will never reach the
functions values f
(-1)
= 1/2 and f
(1) = 1/2, though their graphs
come closer and closer to the points (-1,
1/2) and (1, 1/2) as n
increases. |
|
Then by integrating the series
|
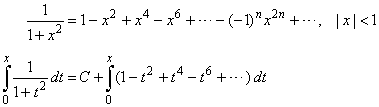
|
|
and since for
x = 0
the integral is zero then, C
= 0 therefore
|
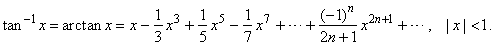
|
|
From where, for x
= 1
|
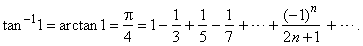
|
| Let
write down the initial sequence of nth
order polynomials, which describe the f
(x) = arctan x
by the above
power series inside the interval of convergence
-1
< x < 1, |
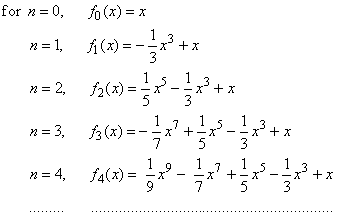 |
| Since
every polynomial above is missing the preceding even degree term, their
coefficient an
-1
= 0 |
| thus, the coordinates
of translations |
|
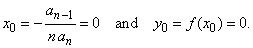 |
|
|
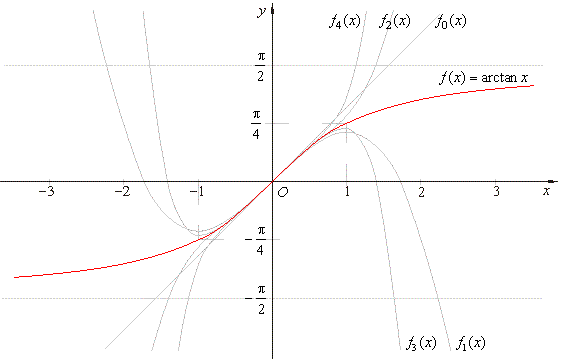
| Therefore,
the polynomials that describe the function
all are
source polynomials of odd degree, as
shows the picture below.
|
|
|
Note that all polynomials in the
series with odd indexes have extreme points at x
= -1
and x =
1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Calculus contents
F |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |