The
quartic
function |
|
The
source
or original quartic
function |
|
The
quartic
functions classification diagram |
|
The
graphs of the quartic functions
types 4/1 . . . 4/6 |
|
|
|
|
|
|
| Quartic
function y
=
a4x4
+ a3x3
+
a2x2
+
a1x + a0 |
| Thus,
y
= a4x4
+ a3x3
+
a2x2
+
a1x + a0
or y
-
y0
=
a4(x
-
x0)4
+
a2(x
-
x0)2
+
a1(x
-
x0), |
 |
 |
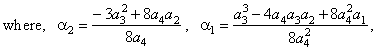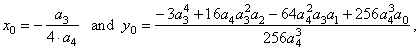| by
setting x0
=
0 and y0
= 0 we get
the source quartic y
=
a4x4
+
a2x2
+
a1x. |
|
|
|
| By
setting the coefficients a2
and a1
of the source quartic to zero interchangeably, obtained is the
basic classification shown in the diagram. |
 |
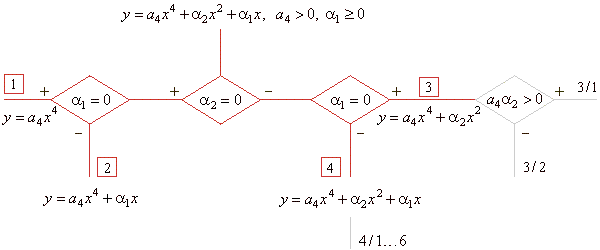| There are
altogether ten types or shapes of graphs of quartic functions. |
|
| The
graphs of the quartic functions
types 4/1 . . . 4/6 |
| Remaining
six types of quartic polynomial satisfy the criteria shown in the
diagram below. |
 |
|
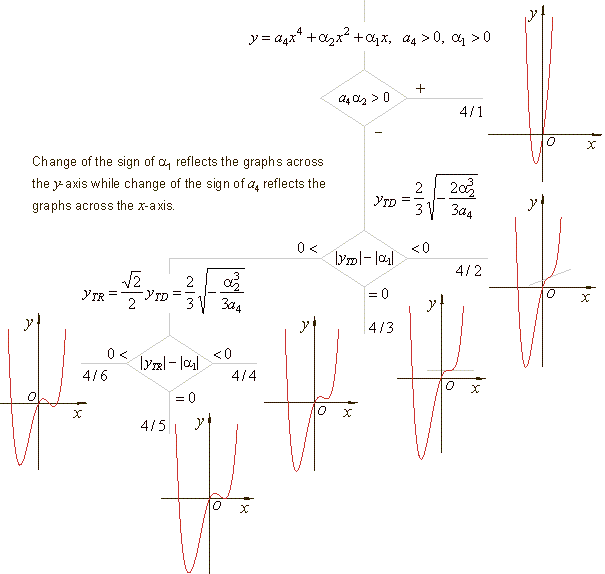| The
roots of the source quartic
y
=
a4x4
+
a2x2
+
a1x
Types,
4/1, 4/2, 4/3 and 4/4 |
 |
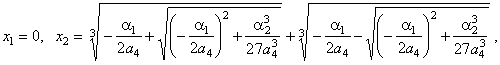| the
roots of the Types,
4/5 and 4/6 |
 |
 |
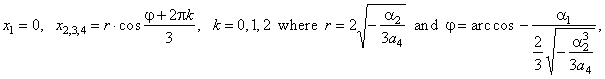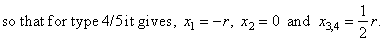| The
abscissa of the turning point of the Types,
4/1, 4/2 and 4/3 |
 |
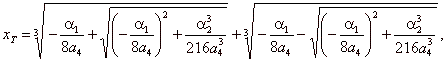| the
abscissas of the turning points of the Types, 4/4,
4/5 and 4/6 |
 |
 |
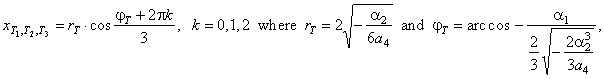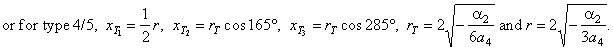| The
abscissas of the points of inflection of the
source quartic of Types 4/2
to 4/6, |
 |
|
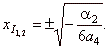| The
roots of the translated quartic Type 4
we get by adding x0
to the solutions of the equation |
| a4x4
+
a2x2
+
a1x
+
y0
= 0. |
|
|
|
|
