|
Translated
cubic functions |
|
Drawing graphs of translated
cubic functions |
|
|
|
|
|
|
|
|
| Cubic
function
y
=
a3x3
+
a2x2
+
a1x + a0 |
| There are three types
(shapes) of cubic
functions whose graphs are shown in the figure below: |
| type
1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0
or y
-
y0
= a3(x
-
x0)3,
-
(a2)2
+ 3a3a1
= 0 or a1
= 0. |
|
| therefore,
its source function y
=
a3x3,
and the tangent line through the point of
inflection is horizontal. |
| type
2/1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0),
where a3a1>
0 |
|
| whose
slope of the tangent line through the point of inflection is
positive and equals a1. |
| type
2/2 |
y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0),
where a3a1<
0 |
|
| whose
slope of the tangent line through the point of inflection is
negative and is equal a1. |
| The
graph of its source function has three zeros or roots at |
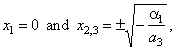 |
|
| and two turning
points at |
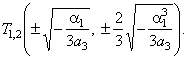 |
|
|
| Translated
cubic functions |
| type
1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3-
x0)3-
x0)3-
x0)3
where, |
|
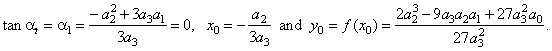 |
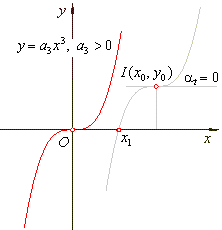 |
|
The
root |
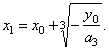 |
The point of inflection I(x0,
y0). |
|
|
|
|
| type
2/1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
+ a1(x
-
x0),
a3
· a1
>
0, |
|
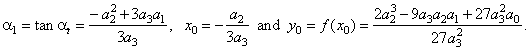 |
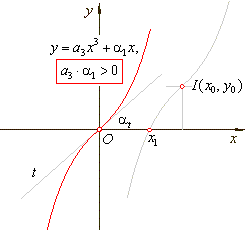 |
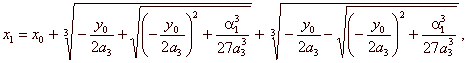 |
I(x0,
y0). |
|
|
|
| |
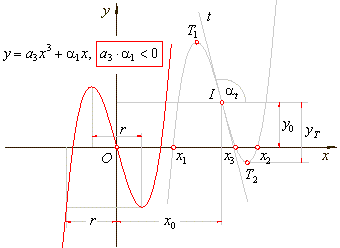
| type
2/2 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
+ a1(x
-
x0),
a3
· a1
<
0, |
|
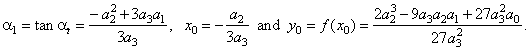 |
 |
| If
| y0
| > |
yT
|
|
|
| |
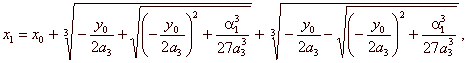 |
| if
| y0
| < |
yT
| |
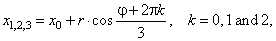 |
|
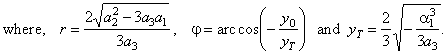 |
|
The turning points |
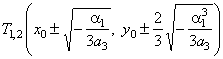 |
The
point of
inflection
I(x0,
y0). |
|
|
|
|
|
|
|
|