|
|
|
|
|
|
|
| The
graphs of the
polynomial functions |
| The
graph of a function ƒ
is drawing on the Cartesian plane, plotted with respect to
coordinate axes, that shows functional relationship between
variables. The points (x,
ƒ (x)) lying on the curve
satisfy this relation. |
| The
polynomial function
f (x) =
y = an
xn
+ an-1
xn-1
+ an-2
xn-2
+
.
. . +
a2
x2
+
a1 x + a0 |
|
y
=
a1x
+ a0
- Linear
function |
|
y
=
a2x2
+
a1x + a0
-
Quadratic
function |
|
y
=
a3x3
+
a2x2
+
a1x + a0
-
Cubic
function |
|
y
=
a4x4
+
a3x3
+
a2x2
+
a1x + a0
-
Quartic
function |
|
y
=
a5x5
+ a4x4
+
a3x3
+
a2x2
+
a1x + a0
-
Quintic
function |
|
- - - -
- - - - - - - - -
- - - - - - - -
- - - - - - - - |
|
| The
source
or original polynomial function |
| Any
polynomial f (x)
of degree n >
1 in the general form, consisting
of n
+ 1 terms, shown graphically, represents translation of its
source (original) function in the direction of the coordinate
axes. |
|
The source polynomial function |
|
fs(x)
= an
xn
+ an-2
xn-2
+
.
. . +
a2x2
+ a1x
|
|
|
| has
n
- 1 terms
lacking second and the constant term, since its coefficients, an-1
=
0
and a0
=
0
while
the leading coefficient an,
remains unchanged. |
| Therefore,
the source polynomial function passes through the
origin. |
| A
coefficient ai
of
the source function is expressed by the coefficients of the general
form. |
|
| Translating
(parallel shifting) of the polynomial function |
| Thus,
to obtain the graph of a given polynomial function f
(x)
we translate (parallel shift)
the
graph of its source function in the direction of the x-axis
by x0
and in the direction of the y-axis
by y0. |
| Inversely,
to put a given graph of the polynomial function beck to the
origin, we translate it in the opposite direction, by taking the
values of the
coordinates of translations with opposite sign. |
|
| Coordinates of translations
and their role in the polynomial expression |
| The
coordinates of translations we calculate using the formulas, |
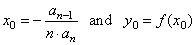
|
| Hence,
by plugging the coordinates of translations into
the source polynomial function fs(x),
i.e., |
|
y
- y0
= an(x
- x0)n
+ an-2(x
- x0)n-2
+
.
. .
+
a2(x
- x0)2
+ a1(x
- x0) |
|
|
| and
by expanding above expression we get the polynomial function in
the general form |
| f
(x) =
y = an
xn
+ an-1xn-1
+ an-2
xn-2
+
.
. . +
a2 x2
+
a1 x + a0. |
| Inversely, by plugging the coordinates of translations into
the given polynomial f
(x)
expressed in the general form,
i.e., |
|
y
+ y0
= an
(x
+ x0)n
+ an-1
(x
+ x0)n-1
+
.
. .
+ a1(x
+ x0)
+ a0 |
|
|
| and
after expanding and reducing above expression we get its source polynomial function. |
| Note
that in the above expression the signs of
the coordinates of translations are already changed. |
|
| The
cubic
function
y
=
a3x3
+
a2x2
+
a1x + a0 |
| Applying
the same method we can examine the third degree polynomial
called cubic function. |
| 1)
Calculate the
coordinates of translations |
| substitute
n
= 3
in |
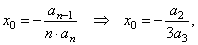 |
|
|
| and |
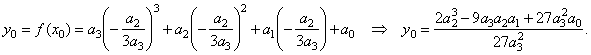 |
|
| 2)
To
get the source cubic function we should plug the coordinates
of translations (with changed signs)
into the general form
of the cubic,
i.e., |
| y
+ y0
= a3(x
+ x0)3
+
a2(x
+ x0)2
+
a1(x
+ x0)
+
a0, |
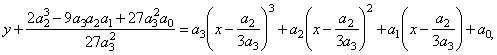 |
| after
expanding and reducing obtained is |
| |
 |
the source
cubic function. |
|
| 3)
Inversely, by plugging the coordinates of translations into the source
cubic |
|
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0), |
|
|
|
after
expanding and reducing we obtain |
|
y
=
a3x3
+ a2x2
+ a1x
+ a0
the cubic function
in the general form. |
| Thus,
y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0), |
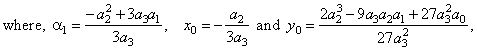 |
| by
setting x0
=
0 and y0
= 0 we get
the source cubic function
y
= a3x3
+
a1x
where a1=
tan at
. |
|
|
|
| Coordinates
of the point of inflection coincide with the coordinates of
translations, i.e., I
(x0,
y0).
|
| The source cubic functions are
odd functions. |
| Graphs of odd functions are
symmetric about the origin that is, such functions change
the sign but not absolute value when the sign of the independent variable is
changed, so that f
(x)
=
-
f (-x). |
| Therefore,
since f (x)
= a3x3
+
a1x
then -
f
(-x)
= -[a3(-x)3
+
a1(-x)]
= a3x3
+
a1x
=
f (x). |
| That
is, change of the sign of the independent variable of a function
reflects the graph of the function about the y-axis,
while change of the sign of a function reflects the graph of the
function about the x-axis. |
| The
graphs of
the translated cubic functions are symmetric about its
point of inflection. |
|
|